Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 90
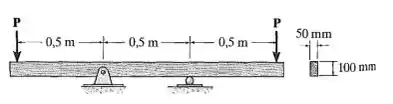
A viga tem a seção transversal retangular mostrada na figura. Determine a maior carga P que pode ser suportada em suas extremidades em balanço de modo que a tensão de flexão na viga não ultrapasse σmáx = 10 MPa.
Passo 1
Falaa! A gente quer a carga máxima que essa viga pode ter sem que a tensão causada pelo momento ultrapasse .
Para achar esse valor, precisamos achar a expressão para a tensão máxima do momento em função de e comparar com essa tensão dada.
Vamos usar essa fórmulinha:
Bora lá!
Passo 2
Nessa fórmula, é o momento de inércia da nossa seção em relação ao eixo . Ele vai ser dado por
é a maior distância entre e a borda da seção, no caso:
Passo 3
Falta , que é o momento máximo na viga.
Precisamos então ver onde o momento nessa viga é máximo. Podemos ver isso pelo diagrama de momento fletor.
Por simetria, as cargas nos dois apoios também valem P. Como a gente só tem cargas pontuais, nós descobrimos o momento em cada ponto nas seções onde tem essas cargas e ligamos tudo por retas. Fica assim: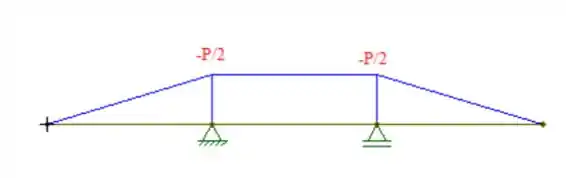
Vemos que o momento máximo vale
(usamos a conveção do diagrama de que para cima temos o momento negativo)
Passo 4
Agora vamos montar nossa tensão máxima e comparar com a tensão dada
Isolando