Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 202
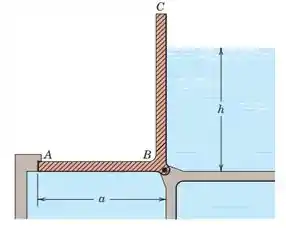
O portão com dobradiças ABC fecha uma abertura de largura b (perpendicular ao papel) em um canal de água. A água também tem livre acesso à parte inferior como o lado direito do portão. Quando o nível da água sobe acima de um certo valor de h, o portão será aberto. Determine o valor crítico de h. Negligencie a massa do portão.
Passo 1
E ai gurizada tudo belezinha???
Em primeiro lugar, teremos de calcular a pressão que atua na parede a partir da água. Observe que a água está sempre agindo normal à superfície, e a expressão para pressão na profundidade h é:
Uma vez que a pressão da água é constante ao longo de toda a largura b, podemos resolver este problema como bidimensional, ou seja, a largura b não tem qualquer efeito no resultado.
Passo 2
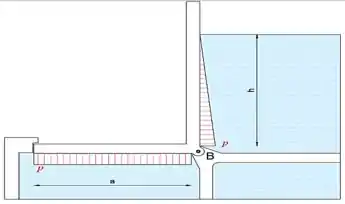
A seguir, isolaremos e desenharemos o diagrama de corpo livre da parede.
Repalimos as cargas distribuídas por suas resultantes atuando no centro de gravidade do triângulo (para carga triangular) e do retângulo (para carga retangular).
Passo 3
Equacionando a soma dos momentos sobre o ponto B a zero, eliminaremos as forças de reação em B de forma que a única incógnita seja a altura h.
Substitua R por seu valor.
Divida os dois lados da equação por p.
A partir daqui, podemos expressar h² como:
Portanto, a altura crítica é: