Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 25
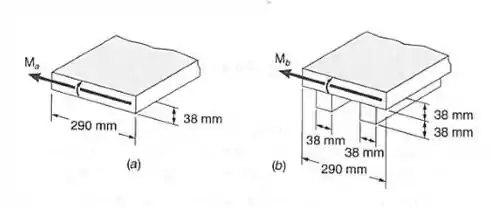
uma prancha de pode ser reforçada pregando-se firmemente dois blocos de , como mostrado. Sabendo-se que e , determinar o maior momento que pode ser aplicado e o correspondente raio de curvatura para:
- A prancha original, sem reforçadores;
- A prancha reforçada com os blocos.
Passo 1
Nossos objetivos são dois, determinar o máximo momento e o raio de curvatura, sabemos que a fórmula da tensão é dada por:
E sabemos que a tensão admissível é determinada da seguinte maneira.
E o raio da curvatura é calculado da seguinte maneira:
Como queremos o raio de curvatura, podemos definir como:
Como o enunciado nos deu o valor de , precisamos determinar o valor de , e sabemos que a relação é dada por:
E como sabemos que o coeficiente de Poisson varia ente , iremos usar o meio termo para a conta, ou seja, , sendo assim teremos que.
E por ser um retângulo, sabemos que a LN ocorre no meio termo da seção, para o item a) e para o item b) iremos recalcular, o que já facilita a nossa vida.
E precisamos do momento de inércia e dos valores de Y, porém isso varia de acordo com a orientação da encurvatura da nossa seção, então para isso iremos dividir o cálculo.
Passo 2
Vamos definir primeiro o momento de inércia e y teremos que:
- Para o item A) a encurvatura ocorre em torno da horizontal, sendo assim teremos que a nossa seção será dada por:
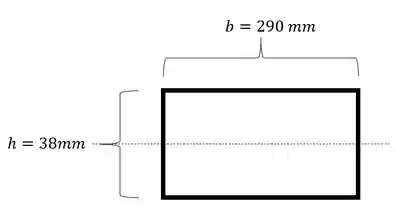
E sabemos que o momento de inercia será calculado por:
E para determinação do y teremos que:
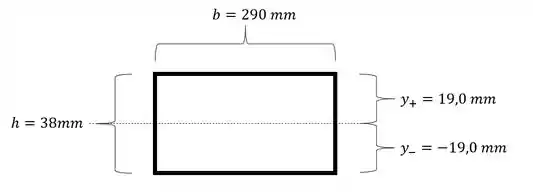
Agora sabemos
E determinando a curvatura, teremos que:
Passo 3
Para o item b) precisamos recalcular a LN, o momento de inércia e o novo momento com reforço, sendo assim teremos que:
Como não temos a LN da nossa barra, precisamos determinar ela. Isso é de suma importância para podermos fazer toda a conta, por isso precisamos seguir um passo a passo para determinar a LN.
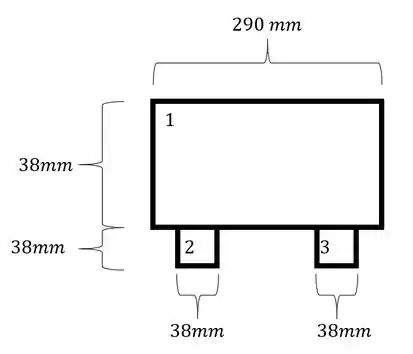
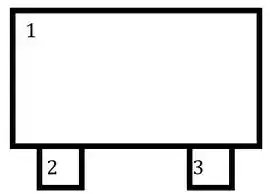
- Primeiro dividir a seção em seções mais simples e numerar elas.
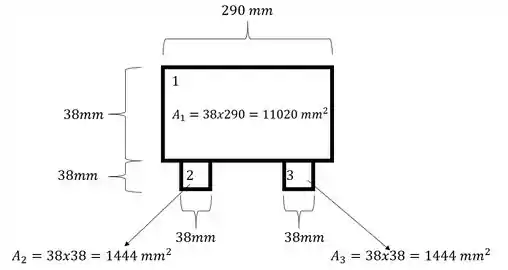
- Em segundo precisamos determinar as áreas de cada uma das regiões e para isso precisamos das medidas do enunciado.
- Em terceiro, precisamos determinar uma origem, porque vai ser com relação com essa origem que vamos determinar a distância dos centroides de cada um dos elementos mais simples. Eu geralmente uso a base do elemento como origem, sendo assim teremos que:
- Por fim precisamos usar a seguinte fórmula para determinar a LN, sendo assim teremos que:
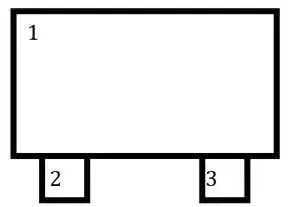
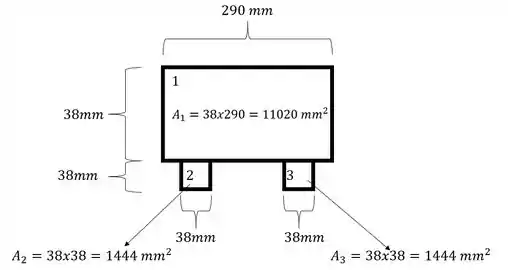
As áreas são:
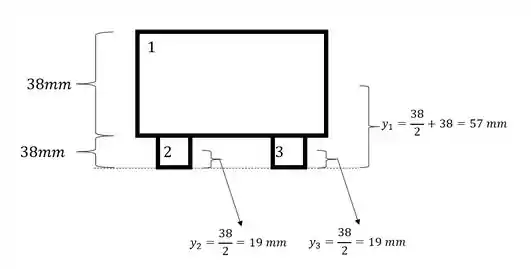
Com isso teremos que:
Substituindo teremos que:
E assim temos que:
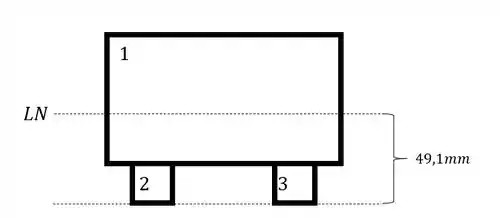
Passo 4
Agora que temos a LN, podemos determinar o momento de inércia, e com isso vamos seguir o seguinte passo a passo.
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
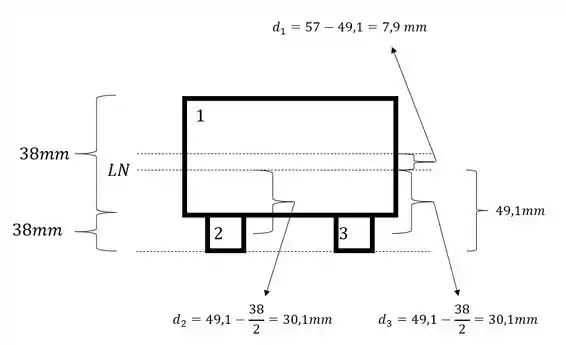
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
- positivo e negativo
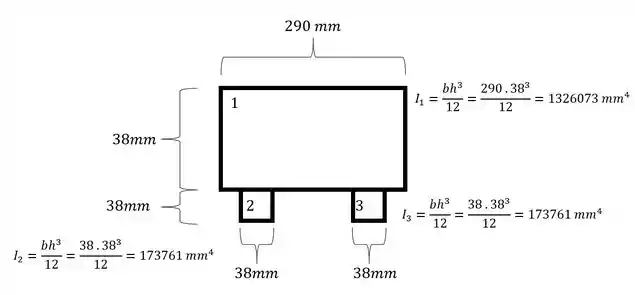
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Sendo assim teremos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:
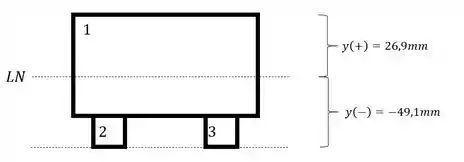
Substituindo, teremos que:
E analisando agora a compressão teremos que:
Substituindo, teremos que:
Como temos as tensões admissíveis, sabemos que ao momento que podemos aplicar será o menor dos que são dados acima, além dos mais, o maior momento dos dois irá romper a menor resistência, enquanto que o menor momento, garante a menor resistência e não afeta a maior, sendo assim teremos que:
E determinando a curvatura, teremos que:
Resposta
- e
- e