Uma torção de uma barra quadrada é removida por fresagem, tal como é mostrado. A barra é então encurvada em torno de eixo horizontal diagonal por um momento . Considerando o caso onde , escrever a máxima tensão na barra na forma , onde é a máxima tensão que poderá ocorrer, se a barra originalmente quadrada tiver sido encurvada pelo mesmo momento , e determinar o valor de .

Passo 1
O nosso objetivo é determinar o valor de k na nossa equação, para isso precisamos lembrar de duas coisas:
Uma é que a nossa fórmula de tensão é dada pela seguinte equação
E a outra é que a fórmula que relaciona as duas situações é dada por:
Em que é a tensão na situação final e é a tensão inicial, considerando o mesmo momento agindo em ambas as situações. Para isso, o mais difícil no nosso problema é determinar o valor do momento de inércia na situação inicial e final, sendo assim teremos que:
Passo 2
Cálculo do momento de inércia na situação inicial:
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
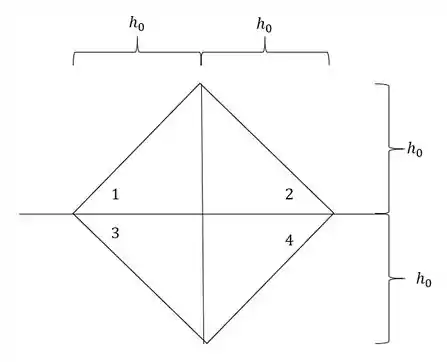


- positivo e negativo
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
As medidas temos que:
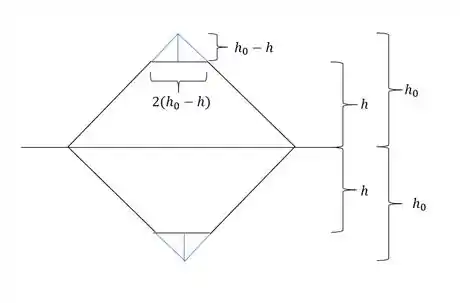
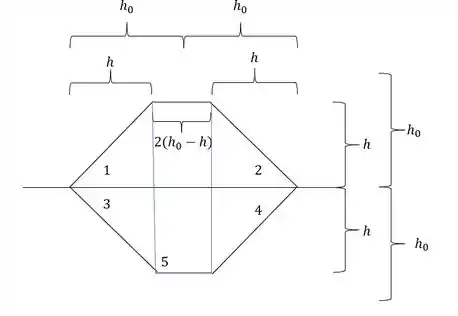
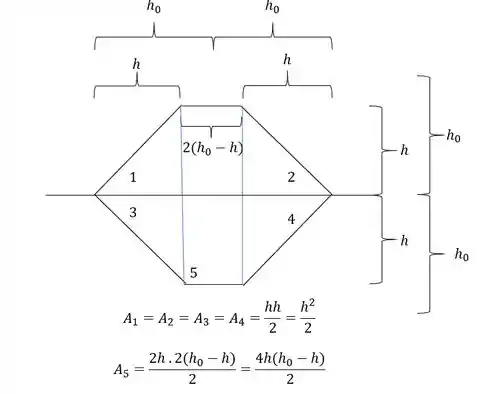

- positivo e negativo
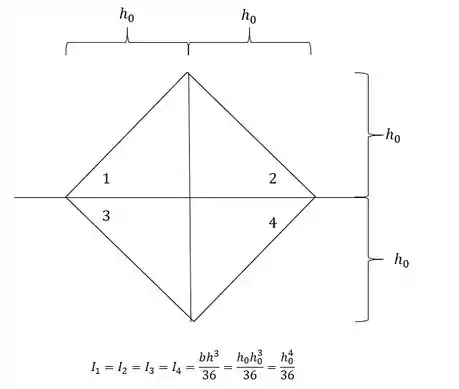
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Determinando o valor de y, temos que:

Calculando a tensão teremos que:
Passo 4
Cálculo do momento de inércia na situação final:
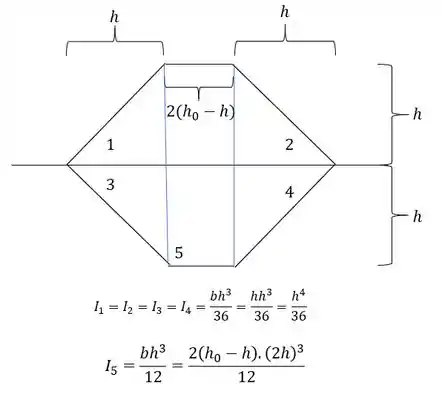
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Sabemos que
substituindo, teremos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Determinando o valor de y, temos que:
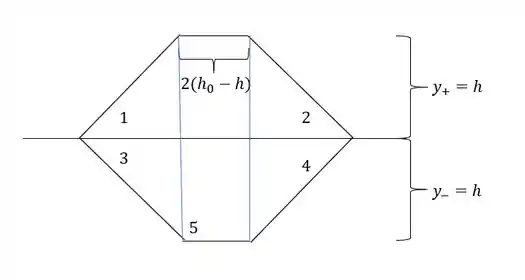
E podemos usar:
Calculando a tensão teremos que:
Como sabemos que a relação é feita por: