Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 135
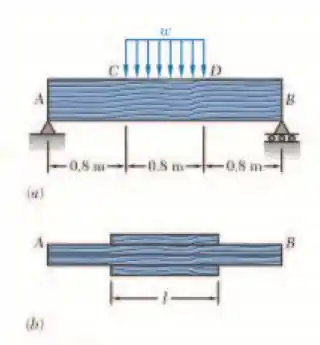
Um projeto preliminar para o uso de uma viga de madeira prismática simplesmente apoiada indicou que seria necessária uma viga com uma seção transversal retangular de 50 mm de largura e 200 mm de altura para suportar com segurança a força mostrada em parte a da figura. Foi decidido substituir essa viga por um viga composta obtida colando-se, como mostra a parte b do figura, quatro peças da mesma madeira da viga original e de seção transversal medindo 50x 50 mm. Determine o comprimento l das duas peças externas de madeira que resultem no mesmo coeficiente de segurança do projeto original
Passo 1
Fala aí gurizada tudo belezinha?? O exercício pede que a gente determine o comprimento l das duas peças externas de madeira que resultem no mesmo coeficiente de segurança do projeto original, então vem comigo :D
Sendo o cisalhamento:
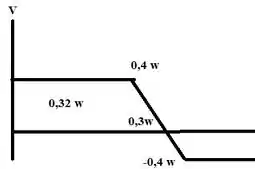
A a C: V= 0,4 w
D a B: V= -0,4 w
Temos agora que determinar as áreas vem comigo :D
Área de A a C temos:
Área de C a E temos:
Esboçando o diagrama de esforço cortante temos:
Passo 2
Agora galerinha devemos determinar os momentos
Fazendo o somatório do momento temos:
Então de A a C temos:
Seja D o ponto onde a espessura muda, temos.
e
Seja F o ponto onde a espessura muda.
Temos então a inércia de::