Um momento deve ser aplicado a uma viga de seção transversal retangular, que é serrado de um tarugo de seção transversal circular. Determinar o raio , para que:
- A máxima tensão seja a menor possível;
- O raio de curvatura da viga seja máximo.
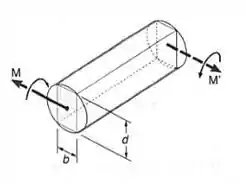
Passo 1
Sabemos que o diâmetro da barra circular pode ser determinado em função das dimensões do tarugo, sendo assim teremos que:
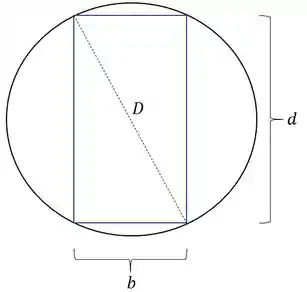
Sabemos que o momento de inércia é dado por:
Sabemos que o modulo resistente é dado por:
E como a tensão é calculada por:
Como queremos a tensão mínima, precisamos ter o máximo, e ter o máximo, significa ter a seguinte razão máxima:
O já sabemos quanto vale, e o , nada mais é que a metade da altura da seção do tarugo, sendo assim teremos que:
Se fizermos a conta do momento resistente, teremos que:
E como você pode lembrar, definimos uma relação entre a base do tarugo, a altura do tarugo, e o diâmetro da barra, e achamos isso aqui:
E perceba que temos o seguinte dado na equação , com isso podemos fazer a seguinte conta:
Substituindo isso no nosso módulo resistente teremos que:
Perceba então que a nossa equação é dada por:
O nosso objetivo é determinar o máximo valor da relação , logo, lembrando o nosso conceito de derivada, se derivarmos o nosso modulo resistente, ele deverá ser igual a zero, para termos o nosso valor máximo. Assim, se derivarmos em função de , e igualarmos a zero, teremos o valor máximo de , sendo assim teremos que:
Se temos o valor máximo de , podemos determinar o máximo , substituindo teremos que:
Como queremos saber exatamente a razão , e fixemos toda a conta para descobrir a tensão mínima, teremos que a conta será dada por:
Logo a razão será dada por:
Passo 2
Para o item b) queremos determinar o raio de curvatura, e sabemos que a equação é dada por:
E se queremos o raio de curvatura máximo, precisamos ter o valor de máximo.
Se elevarmos o momento de inércia ao quadrado, teremos que:
Sabemos que podemos escrever:
Substituindo teremos que:
Derivando teremos que:
Sendo assim teremos que:
Agora que temos o valor de , podemos substituir na seguinte fórmula:
Fazendo a razão, teremos que: