Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 78
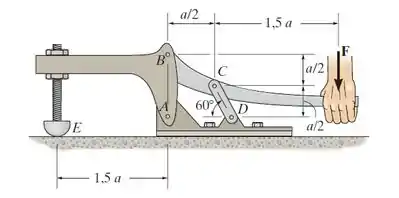
A prensa está sujeita a uma força no punho. Determine a força de prensagem vertical atuando em .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Este tipo de questão nos dá um pequeno trabalho por causa da geometria, mas não é nada do outro mundo.
Devemos determinar a força de prensagem ao aplicarmos uma força vertical na prensa.
Como vocês podem observar na questão, a nossa prensa é composta por duas partes. Temos um braço em que é aplicado a força e contém os pontos e , e a outra parte que contém os pontos , e .
O que temos que fazer agora é esboçar o diagrama de corpo livre de ambos os componentes. Mas, não se esqueçam de substituir cada um dos apoios pelas suas reações.
Começando pelo braço em que atua a força , temos:
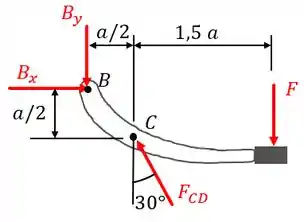
Já para o outro componente, temos:
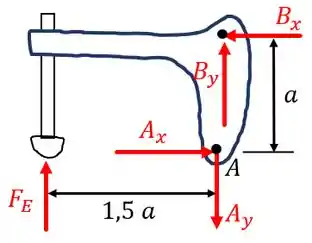
Tenham muito cuidado ao colocarem as reações do pino em ambos os desenhos! Pela lei da ação e reação, eles devem ter sentidos contrários!
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
A sacada para resolver esta questão está em fazer o link da força para o membro que contém a força .
Pelos diagramas vistos no Passo 1, este link é dado pelas reações no pino . Portanto, a nossa primeira tarefa será determinar as reações e . Para isto, será fundamental determinarmos .
Fazendo o somatório de momentos em torno do ponto , temos:
Fazendo o somatório de forças em ambas as direções vertical e horizontal, temos:
Passo 3
Para finalizarmos a questão, vamos relacionar a força com as componentes e que obtivemos no Passo anterior.
Para isto, basta fazermos o somatório de momentos em torno do ponto . Sendo assim, temos:
E assim finalizamos a questão!