Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 32
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro medida a partir de A.
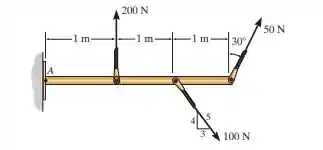
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como está a família?? Tudo na paz?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a força a partir do eixo. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar que, numa determinação de momento, cortante e normal, o cortante é positivo pela direita se ele for para baixo, e que a força aplicada deve ser sempre perpendicular à distância para sabermos o momento.
Quando se analisa o momento, ele é positivo toda vez que estiver girando no sentido anti-horário. Como a gente sabe disso?? Basta usar a regra da mão direita.
Tá, mas agora a gente precisa descobrir nossas variáveis primeiro.
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e achar nossos valores!!