Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 187
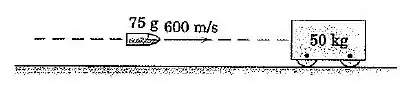
Um projétil de viajando a atinge e se incorpora ao bloco de , que está inicialmente parado. Calcule a energia perdida durante o impacto, Expresse sua resposta como um valor absoluto e como uma percentagem da energia original do sistema .
Passo 1
Vamos usar o princípio da conservação de momento linear. Inicialmente, qual era o momento linera total do sistema?
E depois da colisão, o projétil e o bloco vão andar juntos, de forma que o momento linear do sistema fica:
E como essas duas grandezas tem que ser iguais:
E essa é a velocidade com que conjunto bloco-projétil se move depois da colisão.
Passo 2
Agora vamos pensar em termos de energia, que nesse caso é apenas cinética. Antes da colisão a energia do sistema era:
E depois da colisão os dois corpos estão se movendo com aquela velocidade que nós calculamos:
E então a perda de energia cinética foi:
E em percentagem:
Resolvido!
Resposta
A energia perdida no impacto foi de , ou da energia inicial.