Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 81

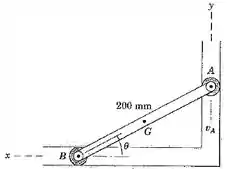
5/81) A extremidade A da barra possui uma velocidade para baixo v A de 2   m / s durante um intervalo de seu movimento . Para a posição em que θ = 30 ° determine a velocidade angular ω de A B e a velocidade de v G do ponto central G da barra . Resolva as equações da velocidade relativa , inicialmente , utilizando a geometria do polígono de vetores e , em seguida , utilizando a álgebra vetorial .

Passo 1

Então galera , como aprendido nesta seção , temos que :

v B = v A + v B / A

A velocidade angular , por sua vez , é dada por :

ω = v B / A B A - = 2 cos ⁡ 30 ° 0,200 = 11,55   r a d / s   c w

Passo 2

Utilizando raciocínio análogo ao do passo anterior , sabemos que :

v G = v A + v G / A

Analisando o diagrama , temos que :

v G = 2 3 = 1,155   m / s

Logo ,

v A = - 2 j m s   ,   v B = v B i   ,   ω A B = ω A B k

v B i = - 2 j + ω A B k x 0,2 cos ⁡ 30 ° i - 0,2 sen ⁡ 30 ° j

A velocidade angular , por sua vez , é dada por :

ω A B = 2 0,1732 = 11,55   r a d / s   c w  

Sendo assim , temos que :

v G = - 2 j + 11,55 k x 0,1 cos ⁡ 30 ° i - 0,1 sen ⁡ 30 ° j

v G = - 2 + 1,00 j + 0,577 i = - j + 0,577 i   m / s

Logo , o seu módulo é dado por :

v G = 1 2 + 0,577 2 = 1,155   m / s

Resposta

v G = 1,155   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.88. A roda gira sobre seu cubo sem deslizar na superfície horizontal. Se a velocidade do centro da roda é V c = 0,6 m s , para a direita, determine as velocidades dos pontos A e B no instante mostr
16.95. A roda está rigidamente fixada à engrenagem A , que está engrenada às cremalheiras D e E . Se D tem uma velocidade V D = 1,8m / s e V E = 3 m / s . Demonstre que é necessário que a roda deslize
72. O trem de engrenagens epicicloidal consiste da engrenagem sol A que está engrenada à engrenagem planetária B. Esta tem um cubo interior com a engrenagem C que está fixo em B e engrenado na engrena
73. Se a barra de ligação AB tem uma velocidade angular ω A B = 4r a d / s no instante mostrado, determine a velocidade do bloco deslizante E nesse instante. Também identifique o tipo de movimento de
16.106. A placa quadrada está restringida dentro das ranhuras em A E B . Quando θ = 30 ° , o ponto A está se deslocando com V A = 8 m s . Determine a velocidade do ponto C nesse instante.