Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 23b

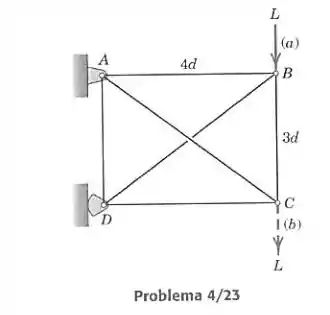
O quadro retangular é composto de quatro elementos perimetrais de duas forças e de dois cabos A C e B D que são incapazes de suportar compressão. Determine as forças em todos os elementos devidas à carga L na posição (b).

Passo 1

Devemos primeiro calcular as forças externas causadas no ponto A e D na treliça. Fazemos as equações de equilíbrio em x e y e do momento em torno de A . Note que o apoio em D só pode causar força para a direita (normal à parede), por conta de seu formato.

∑ F x = 0 ⇒ A x + D x = 0

∑ F y = 0 ⇒ A y - L = 0 ⇒ A y = L

∑ M A = 0 ⇒ D x 3 d - L 4 d = 0 ⇒ D x = 4 3 L ⇒ A x = - 4 3 L

Passo 2

Vamos resolver as equações de equilíbrio em x e y   para cada nó. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração. Os ângulos de inclunação tem seno igual a 3/5 e cosseno igual a 4/5.

Nó B:

Analisando esse ponto, como o cabo B D não pode ser comprimido, pela figura parece que ele também não está sendo tracionado, então assumiremos que B D = 0 .

∑ F x = 0 ⇒ - A B - 4 5 B D = 0 ⇒ A B = 0

∑ F y = 0 ⇒ - B C - 3 5 B D = 0 ⇒ B C = 0

Passo 3

Nó C:

∑ F x = 0 ⇒ - C D - 4 5 A C = 0 ⇒ C D = - 4 5 A C

∑ F y = 0 ⇒ - L + B C + 3 5 A C = 0 ⇒ L = 3 5 A C ⇒ A C = 5 L 3   ( T )

C D = - 4 5 5 L 3 ⇒ C D = - 4 L 3   ( C )

Passo 4

Nó D:

F x = 0 ⇒ D x + 4 5 B D + C D = 0 ⇒ 4 3 L - 4 L 3 = 0         ( O K ! )

∑ F y = 0 ⇒ A D + 3 5 B D = 0 ⇒ A D = 0

Passo 6

Nó A:

∑ F x = 0 ⇒ A x + A B + 4 5 A C = 0 ⇒ - 4 3 L + 4 5 5 L 3 = 0 ⇒ - 4 L 3 + 4 L 3 = 0         ( O K ! )

∑ F y = 0 ⇒ L - A D - 3 5 A C = 0 ⇒ L - 3 5 5 L 3 = 0         ( O K ! )

Como todas as equações foram satisfeitas, nossa suposição inicial estava correta.

Resposta

B D = 0

A B = 0

B C = 0

A C = 5 L 3   ( T )

C D = 4 L 3   ( C )

A D = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

120- Cada uma das estruturas mostradas nas figuras consiste em dois elementos em forma de L ligados por duas hastes rígidas. Para cada estrutura, determine as reações nos apoios e indique se a estrutu
122- A força de 380N é aplicada a alavanca da prensa em C . Sabendo que θ = 90 , determine a ) a força vertical exercida no bloco em D , b ) a força exercida no elemento A B C em B .
127- A prensa mostrada na figura é usada para gravar um pequeno selo em E . Sabendo que o componente vertical da força exercida sobre o selo deve ser 900N , determine a ) a força vertical necessária P
Determine a força exercida no elemento B D e a componente da reação em C .
A haste C D é montada com um colar em D que pode se mover ao longo da haste A B , que foi dobrada em forma de arco de círculo. Para a posição quando θ = 30 ° , determine a a força na haste C D , b a r