Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 33
33- Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em . As conexões são articuladas a estrutura do caminhão em , e . Determine a força fornecida pelo cilindro para sustentar a plataforma na posição mostrada. A massa da plataforma na posição mostrada. A massa da plataforma e das conexões pode ser desprezada em comparação com a massa do caixote de com centro de massa em .
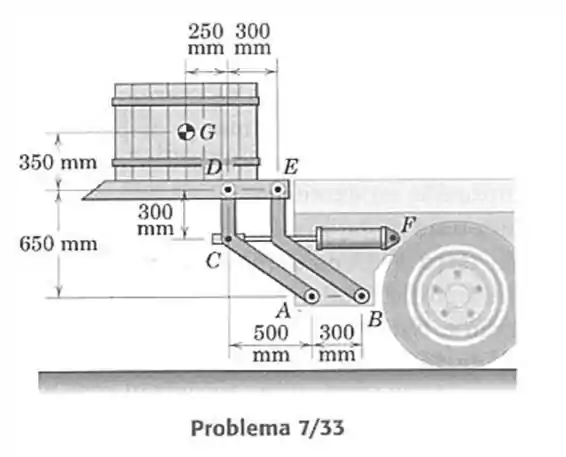
Passo 1
Vamos utilizar a teoria de trabalhos virtuais que nos diz que:
Agora vamos esquematizar as forças presentes no sistema e a geometria das barras.
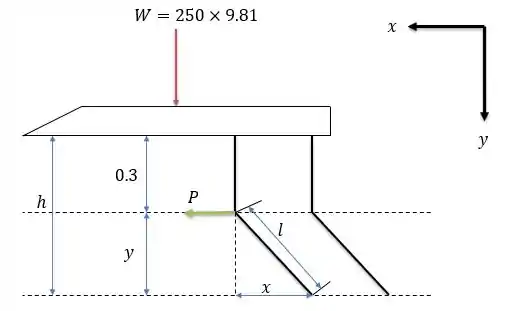
Calculando o peso da caixa nós temos a força :
De forma que o trabalho feito pela força se aplica a distância total , tal que seu trabalho será calculado da seguinte forma:
E o trabalho feito pela força está aplicado a distância de forma que:
Já que as forças encontram nos sentidos positivos do eixo que traçamos.
Passo 2
Analisando o triângulo retângulo formado pelas distâncias e nós teremos a seguinte relação .
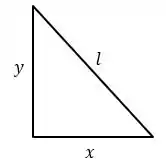
Como é constante e e variáveis pelas nossas forças, temos que se derivarmos a equação a seguinte relação.
Isolando :
Passo 3
Escrevendo então a somatória dos trabalhos virtuais do sistema nós teremos:
Substituindo a relação encontrada no passa anterior:
Como o valor de vale e o de vale vamos substituir e cortar da equação: