Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 3
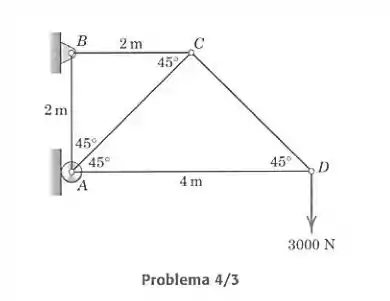
Determine a força em cada elemento da treliça carregada.
Passo 1
Vamos calcular as forças pelo método dos nós, isolando cada pino da treliça. Primeiro vamos às equações externas da treliça, para acharmos os valores de reação de e . Note que o apoio em só causa força para a direita:
Passo 2
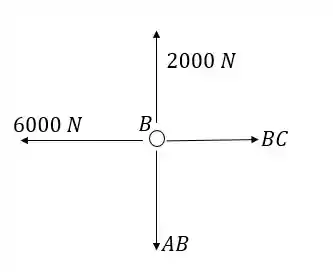
Agora vamos calcular as equações para cada nó. indica compressão e indica tração. Chutaremos os sentidos das forças, e se obtivermos um valor negativo quer dizer que são no sentido contrário.
Nó B:
Passo 3
Nó A:
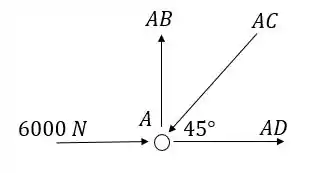
Substituindo na expressão de encontrada:
Passo 4
Nó C:
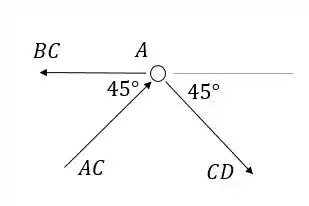
Ainda temos mais equações, mas já achamos todos os valores que queríamos.
Resposta
Exercícios de Livros Relacionados
Determine a força em cada elemento da treliça carregada.
Calcule as forças nos elementos C G e C F para a treliça mostrada.
Determine a força em cada elemento da treliça carregada.
Determine a força nos elementos B E e C E da treliça carregada.
Determine as forças nos elementos A F , B E , B F e C E da treliça carregada.