Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 119

Quatro forças são aplicadas no componente de máquinas A B C D E como mostra na figura. Substitua essas forças por um sistema de força-binário equivalente em A .

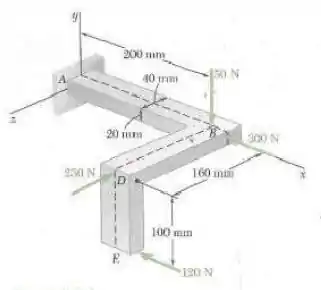
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como estamos trabalhando em três dimensões, vamos escrever as forças em forma de vetor. Vou retratar cada força com a nomenclatura do ponto de ação. Temos que:

B x = - 300   i

B y = - 50 j

D z = - 250 k

E x = - 120 i

Essas são as forças agindo no sistema. Agora vamos calcular a força resultante:

R = ∑ F

R = B x + B y + D z + E x

R = - 300   i - 50 j - 250 k - 120 i

R = - 420 i - 50 j - 250 k   N

Passo 2

Agora, vamos calcular o momento resultante em A sobre cada eixo. Para o eixo x , temos:

M x = ∑ M x

M x = 0

Para o eixo y , temos:

M y = ∑ M y

M y = 250 0,2 - 120 0,16

M y = 30,8   N ⋅ m

Para o eixo z , temos:

M z = ∑ M z

M z = - 120 0,1 - 50 ( 0,2 )

M z = - 22   N ⋅ m

Portanto, podemos retratar o momento resultante total como:

M = M x + M y + M z

M = 0 i + 30,8 j - 22 k   N ⋅ m

Resposta

R = - 420 i - 50 j - 250 k   N

M = 0 i + 30,8 j - 22 k   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os diagramas de força cortante e de momento fletor para a viga.
Determine os diagramas de força cortante e de  momento fletor para a viga.
Determine os diagramas de força cortante e de momento fletor para a viga.
Determine a força normal, a força cortante e o momento fletor no elemento curvo em função de u, onde 0 °θ90 ° .
Determine a força normal, a força cortante e o momento fletor no elemento curvo em função de P. A força P atua em um ângulo constante ϕ .