Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 37
A barra AC sustenta duas cargas de 400 N, tal como mostra a figura. Os roletes A e C estão apoiados em superfícies sem atrito, e um cabo BD é preso em B. Determine a tração no cabo BD, a reação em e a reação em .
Passo 1
Tá legal, vamos lá! A primeira coisa que fazemos nesse tipo de exercício é desenhar o DCL do sistema:
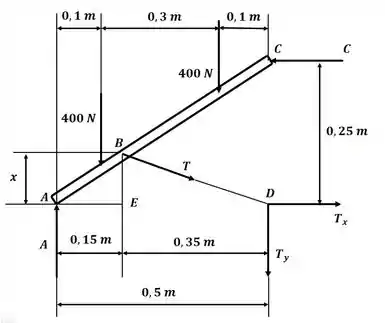
Antes de qualquer coisa, precisamos descobrir o valor de , para podermos decompor a força de tração em suas componentes e , então por semelhança entre os triângulos ABE e ACD, temos:
Passo 2
Beleza, agora podemos aplicar o somatório de forças na direção :
E agora, aplicando o somatório de momento em relação ao ponto A, temos:
Podemos escrever o termo em função de com o auxílio do triângulo BDE, então temos:
Substituindo esse valor e o valor de encontrado, podemos reescrever a equação de momento como:
Isolando e resolvendo:
Substituindo esse valor na equação para :
Passo 3
Agora, aplicando o somatório de forças na direção :
Substituindo o valor encontrado para no passo 2, isolando A e resolvendo, temos:
E, substituindo o valor de na relação encontrada no passo 2, obtemos o valor de :