Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 58

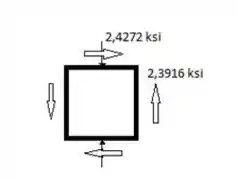
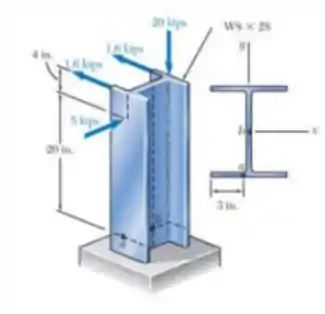
Quatro forças são aplicadas a um perfil de aço laminado W8 x 28, conforme mostra a figura. Determine as tensões principais e a tensão de cisalhamento máxima no ponto b.

Passo 1

E ai gurizada tudo certo? Temos que calcular forças e pares na seção contendo ponto de interesse, vamos considerar o esboço ;)

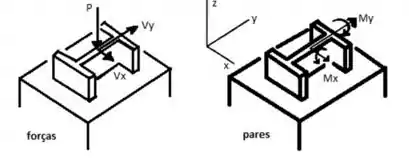
Temos que:

P = 20 k i p s     V x = - 3,2 k i p s       V y = 5 k i p s

Agora vamos determinar os momentos :D

M x = - 20 5 - 4,03 20 = - 180,6 k i p s ∙ i n

M y = - 20 + 4 3,2 = - 76,8 k i p ∙ i n .

Passo 2

Propriedades da seção: A = 8,24 i n 4     d = 8,06 i n .       b f = 6,54 i n .       t f = 0,465 i n .

t w = 0,285 i n .     I x = 98,0 i n 4     I y = 21,7 i n 4

Ponto b: x b = 0       y b = 0

σ b = - P A + M x y b I x + M y X b I y = - 20 8,24 + 0 + 0 = - 2,4272 k s i

Tensão de cisalhamento no ponto b devido ao V x :

τ x z = 0

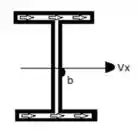
Passo 3

Tensão de cisalhamento no ponto b devido ao V y :

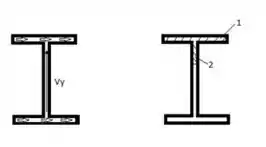
Agora devemos determiner as seções :D

Q = Σ A y - = 13,3597 i n 3

τ b = V y Q I x t w = 5 13,3597 98,0 0,285 = 2,3916 k s i

σ a v e = - 2,4272 + 0 2 = - 1,2136 k s i

R = - 2,4272 - 0 2 2 + 2,3916 2 = 2,6819 k s i

σ M A X = σ + R                                         σ M A X = 1,468 k s i

σ M I N = σ a v e - R                                       σ M I N = - 3,90 k s i

τ M A X = R                                                                       τ M A X = 2,68 k s i

Resposta

σ M A X = σ + R                                         σ M A X = 1,468 k s i

σ M I N = σ a v e - R                                       σ M I N = - 3,90 k s i

τ M A X = R                                                                       τ M A X = 2,68 k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A cabine de teleférico e seus passageiros pesam 7,5 kN, e o centro de gravidade do conjunto está em G. O braço de suspensão AE tem área da seção transversal quadrada de 38 mm por 38 mm e está preso po
O suporte de aço é usado para ligar as extremidades de dois cabos. Se a força P=2,5k N for aplicada, determine a tensão normal máxima no suporte. O suporte tem espessura de 12m m e largura de 18m m .
A força vertical P age na parte inferior da capa cujo peso é desprezível. Determine a distância máxima d até a borda na qual aquela força pode ser aplicada de modo a não produzir nenhuma tensão de com