Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 44

A força vertical P de intensidade 60lb é aplicada no ponto A da manivela. Sabendo que o eixo BDE tem um diâmetro de 0,75in., determine as tensões principais e a tensão de cisalhamento máxima no ponto H localizado no topo do eixo e afastado de 2in. à direita em relação ao apoio D.

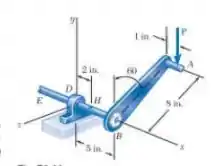
Passo 1

Sistema força-par no centroide na seção contendo ponto H é esboçado abaixo, vem comigo :D

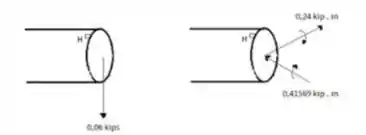
Temos então que determinar o momento vem comigo!!!

F x = 0 ,                   V y = - 0,06 k i p s ,           V z = 0

M z = - 5 - 2 + 1 0,06 = - 0,24 k i p ∙ i n .

M x = - 8 s i n 60 ° 0,06 = - 0,41569 k i p ∙ i n .

d = 0,75 i n .             c = 1 2 d = 0,375 i n .

I = π 4 c 4 = π 4 0,375 4 = 15,5316 x 10 - 3 i n 4

J = 2 I = 31,063 x 10 - 3 i n 4

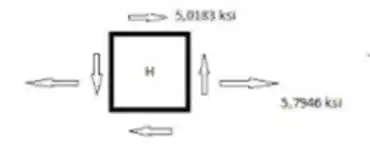
Passo 2

No ponto H, temos a seguinte tensão:

σ H = - M z y I z = - - 0,24 0,375 15,5316 x 10 - 3 = 5,7946 k s i

τ H = T c J = 0,41569 0,375 31,063 x 10 - 3 = 5,0183 k s i  

Usando círculo de Mohr. σ a v e = 1 2 σ H = 2,8973 k s i  

R = \ σ H 2 2 + τ H 2 = 5,7946 k s i

σ a = σ a v e + R                       σ M A X = 8,69 k s i

σ b = σ a v e - R                     σ M I N = - 2,90 k s i    

Passo 3

t a n 20 p = 2 τ H σ H = 2 5,0183 5,7946 = 1,7321

θ a = 30,0 °               θ b = 120,0 °

τ M A X = R                                                   τ M A X = 5,79 K S I

Resposta

5,79 K S I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Várias forças são aplicadas ao tubo montado conforme a figura. Sabendo que o tubo tem diâmetros interno e externo iguais a 40,9mm e 48,3mm, respectivamente, determine as tensões normal e de cisalhamen
Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.
Resolva o Problema 8,45 considerando que h =304,8mm
Duas forças são aplicadas a uma pequena coluna BD conforme mostrado. Sabendo que a porção vertical da coluna tem uma seção transversal de 1,5x2,4in., determine as tensões principais, os planos princip