Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 29

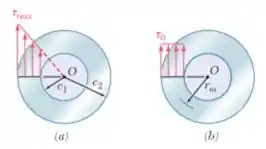
Embora a distribuição exata das tensões de cisalhamento em um eixo cilíndrico vazado seja como mostra a Fig. P3.29a, pode-se obter um valor aproximado para T m á x considerando que as tensões são uniformemente distribuídas sobre a área A da seção transversal, como mostrar a Fig. P3. 29b, e supondo ainda que todas as forças de cisalhamento elementares agem a determinada distância do ponto O dada pelo raio médio da seção transversal 1 2 ( c 1 + c 2 ). Esse valor é valor uma aproximação de t 0 = T / A r m á x em que T é o torque aplicado. Determine relação t m á x / t 0 + em que t m á x é tensão de cisalhamento exata e t 0 é a tensão aproximada para para valores da relação c 1 / c 2 + respectivamente iguais a 1,00; 0,95; 0,75; 0,50 e 0.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine relação t m á x / t 0 +

Para um eixo oco

τ m a x = T c 2 J = 2 T c 2 π c 2 4 - c 1 4 = 2 T c 2 π c 2 2 - c 1 2 c 2 2 + c 1 2 = 2 T c 2 A c 2 2 + c 1 2

Por definição

τ 0 = T A r m = 2 T A c 2 + c 1

Dividindo

τ m a x τ o = c 2 c 2 + c 1 c 2 2 + c 1 2 = 1 + c 1 / c 2 1 + c 1 / c 2 2

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste sólida AB tem um diâmetro d A B = 60m m e é feita de aço para o qual a tensão de cisalhamento admissível é de 85 MPa. O tubo CD, que tem o diÂmetro externo de 90 mm e espessura de parede de 6
Resolva o problema 3.17 considerando que a direção de T c seja invertida.PROBLEMA 3.17 O eixo sólido mostrado é formado por um latão para cuja tensão de cisalhamento admissível é de 55 MPa. Negligenci
Um torque de T = 1000 N/m é aplicado de D, como mostra a figura. Sabendo que diâmetro do eixo AB é de 56 mm e que diâmetro do eixo CD é de 42 mm, determine a tensão de cisalhamento máxima no(a)eixo AB
A haste sólida AB tem um diâmetro dAB = 60 mm. O tubo CB tem um diâmetro externo de 90 mm e parede com 6 mm de espessura. Sabendo que ambos a haste e o tubo são feitos de aço e para o qual a tensão de
Sob condições normais de operação. um motor exerce um torque de intensidade T F = 1200 lb ⋅ in. em F, Sabendo que r D = 8 in., r G =3 in. e que a tensão de cisalhamento admissível é 10,5 ksi em cada e