Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 85b
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal, são firmemente pregadas juntas,
como mostrado, para formar uma coluna. Sabendo-se que para o tipo de madeira usado
E=12GPa e que a tensão admissível a compressão, na direção paralela as fibras, é de
10MPa, determinar a carga centrada admissível quando o comprimento efetivo da coluna é de:(a)2,4m;(b)4,35m
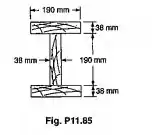
Passo 1
Fala meus projetistas de colunas, tudo certo?
Temos mais um projetinho de coluna de madeira centrada, e aqui a coluna é do tipo e o cálculo é diferente de uma coluna retangular, vem comigo que eu mostro!
Aqui para o nosso item b. vamos calcular novamente alguns parâmetros, a geometria é a mesma, porém os limites são diferentes e vão nos levar a cálculos diferentes mais a frente, tá?
A gente calcula primeiro o parâmetro , que é dado por:
Onde:
é a tensão admissível dada no enunciado.
E vamos comparar o parâmetro abaixo com , avaliando alguns limites para o mesmo que nos darão cálculos diferentes para as tensões que levam ao peso admissível:
Onde:
é o comprimento efetivo da coluna e é o raio de giração.
Lembrando que:
Temos 3 limites para avaliar, o primeiro caso é:
Se estiver nesses limites a coluna é curta e traremos as fórmulas da tensão para esse caso. Para colunas intermediárias temos o nosso segundo caso:
E para colunas longas temos o último caso:
Se por acaso não estiver contido nesses limites a coluna não pode ser projetada. Por fim traremos o seguinte para o peso admissível.
Passo 2
Vamos lá ao cálculo do nosso parâmetro K:
E agora para o raio de giração vamos avaliar a figura:
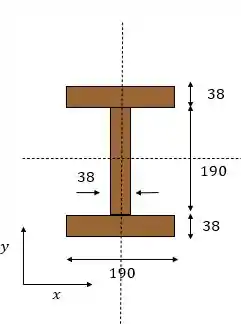
Com as dimensões da figura vamos aos cálculos, e aqui vamos escolher o eixo que é o eixo fraco pra esse tipo de seção e o seu momento de inércia é dado por:
Com:
E:
Substituindo na fórmula temos:
E para o raio de giração também precisamos da área que é dada por:
Enfim temos:
E enfim nosso parâmetro para o item b. onde temos
Temos então uma coluna classificada como longa pelos limites:
Pelos limites apresentados é classificada como coluna intermediária.
Passo 3
Para esse tipo de coluna a formulação das tensões vai ficar:
E substituindo nossos valores temos:
E como falamos lá no passo 1, a relação do peso admissível e a tensão admissível são dados por:
E substituindo:
E em