Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 14
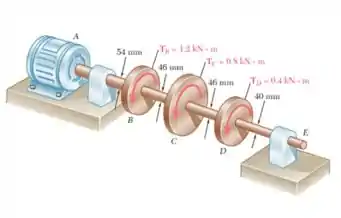
Para reduzir a massa total do conjunto do Problema 3.13, está sendo considerado um novo projeto no qual o diâmetro do eixo BC será menor. Determine o menor diâmetro do eixo BC para o qual o valor máximo da tensão de cisalhamento no conjunto não será aumentado.
Passo 1
E aí, tudo belezinha? Para que conseguir resolver esta questão precisamos consultar as respostas do problema 3.13 para obter as tensões máximas de cisalhamento nas partes AB, BC e CD para ter o eixo onde o maior valor máximo de cisalhamento é de , que ocorre em AB.
Ajuste o diâmetro de BC para obter o mesmo valor de tensão.
Resposta
Então gurizada, com base nas informações e resultados que chegamos vimos que o no novo projeto o diâmetro da base terá , reduzindo em .
Exercícios de Livros Relacionados
O torque T = 900 N/m é o aplicado ao eixo AB do trem de engrenagens mostrando. Sabendo que tensão de cisalhamento admissível é de 80 MPa, determine o diâmetro necessário para o (a) eixo AB , (b) eixo
Os dois eixos de seção transversal cheia estão conectados por engrenagens, como mostra figura. são feitos de um aço para o qual a tensão de cisalhamento admissível é de 58,6 MPa. Sabendo que o torque
Para o trem de engrenagens mostrando, os diâmetros dos três eixos de seção transversal cheia são: d A B = 20mm d C D =25mm d E F =40mmSabendo que a tensão de cisalhamento admissível para cada eixo é d
Embora a distribuição exata das tensões de cisalhamento em um eixo cilíndrico vazado seja como mostra a Fig. P3.29a, pode-se obter um valor aproximado para T m á x á considerando que as tensões são un
Um torque T de 750k N * m é aplicado a um eixo vazado com a seção transversal mostrada na figura e uma espessura de parede uniforme de 6 mm. Desprezando o efeito das concentrações de tensão, determine