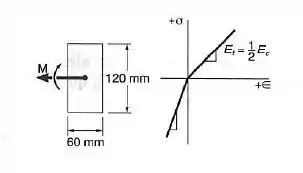
A viga retangular mostrada é feita de um plástico, cujo módulo de elasticidade à tração é metade do valor à compressão. Para um momento fletor de , determinar a máxima: (a) tensão de tração; (b) tensão de compressão.

Primeiro vamos encontrar a localização da linha neutra. Podemos fazer isso montando a equação de equilíbrio de momento estático. Temos essa seção:

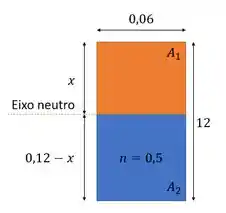
A soma de momentos em torno do eixo neutro deve ser nulo. Cada momento é o produto entre a área e a distância entre o eixo neutro e o centroide de cada área.

Lembrando que a gente tem que usar o valor de para a seção em que há tração, a equação fica assim:

Resolvendo para (escolhendo a raiz positiva):

Vamos calcular os momentos de inércia. Como a gente não tem, de fato, materiais diferentes, mas somente valores diferentes para tração e compressão, calculamos os momentos de cada área:

E somamos tudo:

a) Queremos calcular a tensão máxima de tração. Agora a gente precisa usar o fator . Fica assim:

b) Queremos calcular agora a tensão máxima de compressão. Fica assim: