Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 167

Resolva o Problema 15.166 admitindo que a direção da velocidade relativa u seja invertida, de modo que a porção B D esteja sendo retraída.

Passo 1

Bora pra questão 167 agora, meus caros (as)!

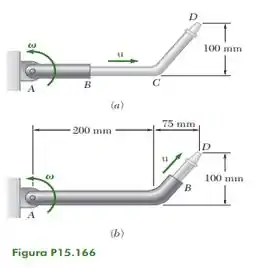
Bom! Pela figura do enunciado, a gente tem que...

r → D / A = 275   m m i ^ + 100   m m j ^

E para obter a aceleração do ponto D , basta usar a fórmula abaixo...

a D = α k ^ × r D / A - ω 2 r D / A

Como ω = 2,4   r a d / s , então...

a D ' = α k ^ × r D / A - ω 2 r D / A

a D ' = - ( 2,4   r a d / s ) 2 [ 275   m m i ^ + 100   m m j ^ ]  

a D ' = - ( 1584   m m / s 2 ) i ^ - ( 576   m m / s 2 ) j ^

Quanto à aceleração do ponto D relativo ao braço A B , temos que...

a D / A B = 0

Passo 2

Quanto ao comprimento do braço C D , esse é dado por...

C D = 100   m m 2 + 75   m m 2

C D = 150   m m

Agora se liga! A velocidade do ponto D relativo ao ponto A , é dada por...

v D / A B = u = ( 250   m m / s ) i ^

Escrevendo em termo dos versores para a barra A B para o segundo caso...

v D / A B = 250   m m / s 150   m m [ 75   m m i ^ + 100   m m j ^ ]

v D / A B = [ 125   m m / s i ^ + 166,67   m m / s j ^ ]

Passo 3

Quanto à aceleração de Coriolis, ela é dada por...

2 ω k ^ × v D / A B

Sendo assim, para o primeiro caso, temos que...

2 ( 2,4   r a d / s ) k ^ × ( 250   m m / s ) i ^ = ( 1200   m m / s ) j ^

E para o segundo caso, por sua vez...

2 ( 2,4 ) k ^ × [ 125   i ^ + 166,67   j ^ ] = - ( 80 0   m m / s 2 ) i ^ + 600   m m / s 2 j ^

a) Desse modo, para obter a aceleração final do primeiro caso, basta usar a fórmula abaixo...

a D = a D ' + a D / A B + 2 ω k ^ × v D / A B

a D = - ( 1584   m m / s 2 ) i ^ - ( 576   m m / s 2 ) j ^ + ( 1200   m m / s ) j ^

a D = - ( 1584   m m / s 2 ) i ^ + ( 624   m m / s ) j ^

Escrevendo em módulo e ângulo...

a D = - 1584   m m / s 2 2 + 62 4   m m / s 2 2 ∠ tan - 1 ⁡ 624 - 1584

a D = 1702,48   m m / s 2 ⦣ 21,5 °

b) Já para o segundo caso, temos que...

a D = a D ' + a D / A B + 2 ω k ^ × v D / A B

a D = - ( 1584   m m / s 2 ) i ^ - ( 576   m m / s 2 ) j ^ - ( 800   m m / s 2 ) i ^ + 600   m m / s 2 j ^

a D = - ( 23 84   m m / s 2 ) i ^ + ( 24   m m / s ) j ^

Escrevendo em módulo e ângulo...

a D = - 23 84   m m / s 2 2 + 24   m m / s 2 2 ∠ tan - 1 ⁡ 24 - 23 84

a D = 2384,12   m m / s 2 ⦣ 3,24 °

Resposta

a)

a D = 1702,48   m m / s 2 ⦣ 21,5 °

b)

a D = 2384,12   m m / s 2 ⦣ 3,24 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa quadrada com 500m m de lado está articulada nos pontos A e B de um grampo em U . A placa gira à taxa constante ω 2 = 4r a d / s em relação ao grampo, que, por sua vez, gira à taxa constante
O rotor de um motor elétrico tem a velocidade de 1.800 rpm quando a energia é desligada. O rotor é então observado até alcançar o repouso após executar 1.550 rpm. Considerando o movimento uniformement
Um ventilador de um motor de um automóvel gira em um eixo horizontal paralelo a direção de movimento do automóvel. Quando visto da retaguarda do motor, observa-se que o ventilador gira no sentido horá
Um ventilador de um motor de um automóvel gira em um eixo horizontal paralelo a direção de movimento do automóvel. Quando visto da retaguarda do motor, observa-se que o ventilador gira no sentido horá
Um tambor de 100 mm de raio está preso rigidamente a um cilindro de 180 mm de raio. Uma corda é enrolada ao redor do tambor e sua extremidade E é puxada para a direita com velocidade constante de 400