Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 99
Descreva o centrodo espacial e o centrodo corporal da barra ABD do Problema 15.84. (Dica: o centrodo corporal não precisa estar sobre uma parte física da barra.)
Passo 1
Bora pra questão 99 agora, meus caros (as)!
E já sabe, né! Nada melhor do que uma figura pra ajudar a entender uma questão.
Vamos fazer um esboço destacando vetorialmente as velocidades e posicionando eixos coordenadas na figura acima, pra entender melhor o que está acontecendo...
Aqui está, nossa bela imagem...
Passo 2
Bom! A gente tem que aponta para a esquerda...
E aponta para baixo...
é o centro de rotação instantâneo da nossa figura. E suas coordenadas, pelo que podemos ver, são...
E aplicando o teorema de Pitágoras, temos que...
Ou seja, o centrodo espacial é um quarto de círculo com centro em e raio de
Passo 3
Agora, vamos esboçar, por exemplo, o que acontece quando tá na horizontal...
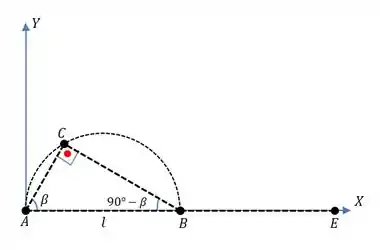
Aí nesse caso, as coordenadas do centro de rotação vão ser dadas por...
Só que...
Logo;
Já é igual à...
Agora dá uma olhada no triângulo abaixo, em vermelho...
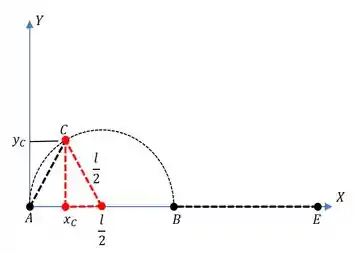
Baseado nele, aplicando Pitágoras, temos que...
Como...
Então...
Ou seja, o centrodo corporal é um semicírculo com de raio, com centro entre e !
Resposta
O centrodo espacial é um quarto de círculo com centro em e raio de e o centrodo corporal é um semicírculo com de raio, com centro entre e .