Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 86

Resolva o Problema 16.67 utilizando o método do centro instantâneo de velocidade nula.

Passo 1

Precisamos começar por relembrar o problema. É importante que voltem para revisar as informações.

A questão nos dava uma bicicleta que possui uma velocidade v = 1,2   m / s e a sua roda traseira possuía uma velocidade ω = 3   r a d / s . Como o ponto de contato da roda com o piso desliza, ela possui uma velocidade. A questão nos pede para determinar esta velocidade.

A análise do centro instantâneo de velocidade nos diz que:

v = ω r

Em que ω é a velocidade angular ao redor do ponto de fixação e a distância r é a distância do nosso ponto fixo até o ponto de análise.

Então, para podermos determinar a velocidade, precisamos começar por encontrar o centro instantâneo de velocidade nula.

Passo 2

Se analisarmos a roda, teremos o seguinte diagrama:

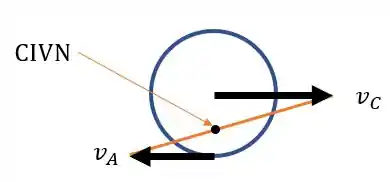
O centro instantâneo de velocidade está localizado entre o centro da roda e o ponto A, pois há uma mudança no sentido da velocidade. Se a gente analisar a geometria do problema, dando um zoom nesta região do CIVN, temos:

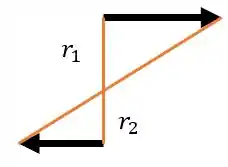
Portanto, sabemos que r 1 + r 2 = 0,65 m , pois é o raio da roda. Para descobrirmos que é r 1 , basta aplicarmos a equação do Passo 1, portanto,

v C = ω r 1

1,2 = 3 r 1

r 1 = 0,4   m

Logo, r 2 = 0,25 m . Desta forma, sabemos que a velocidade do ponto A será:

v A = ω r A

v A = 0,75   m / s

Resposta

v A = 0,75   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.49. No sistema de engrenagens planetárias mostrado na figura, o raio da engrenagem central A é a, o raio das engrenagens planetárias é b e o raio da engrenagem externa E é a +-2b. A velocidade angu
15.51. O braço AB gira com uma velocidade angular de 20 rad /s no sentido anti-horário. Sabendo que a engrenagem C é estacionária, determine (a) a velocidade angular da engrenagem B, (b) a velocidade
15.51. O braço AB gira a uma velocidade angular de 42 rpm no sentido horário. Determine a velocidade angular requerida da engrenagem A para que (a) a velocidade angular da engrenagem B seja de 20 rpm
15.50. A engrenagem A gira com uma velocidade angular de 120 rpm no sentido horário. Sabendo que a velocidade angular do braço AB é 90 rpm no sentido horário, determine a velocidade angular correspond
15.54. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrad