Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 22

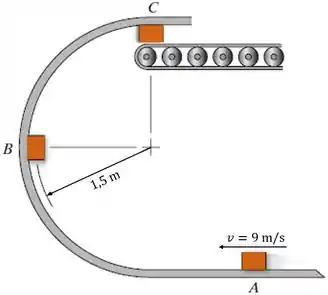
A caixa de 1 kg desliza na rampa circular lisa. Se a caixa tem uma velocidade de 9 m/s em A , determine a velocidade da caixa e a força normal atuando sobre a rampa quando a caixa está localizada em B e C . Suponha que o raio de curvatura da trajetória em C ainda é 1,5 m.

Passo 1

O enunciado nos dá as seguintes informações:

Massa da caixa: m = 1 kg;

Rampa lisa: força de atrito desprezível;

Velocidade em A : v A = 9 m/s;

Raio de curvatura: ρ = 1,5 m.

Devemos determinar a velocidade da caixa e a força normal atuando sobre a rampa quando a caixa está localizada em B e C .

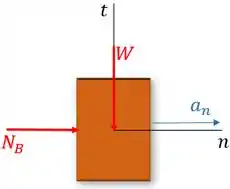
Inicialmente, vamos desenhar o diagrama de corpo livre da caixa para os pontos B e C , respectivamente.

Passo 2

Primeiramente, vamos analisar os dados no Ponto B :

Aplicando o Princípio do Trabalho e Energia, temos

T 1 + ∑ U 1 - 2 = T 2

onde

T 1 = 1 2 m v A 2 = 1 2 1 9 2 = 40,5

T 2 = 1 2 m v B 2 = 1 2 ( 1 ) v B 2

∑ U 1 - 2 = - W y = - 1 9,81 1,5 = - 14,715

Substituindo esses valores na equação inicial, obtemos

40,5 - 14,715 = 0,5 v B 2

v B 2 = 51,57

v B = 7,18   m / s

Agora, utilizando a Equação do Movimento, temos

∑ F n = m a n

N B = m a B

N B = ( 1 ) a B

Sabemos que

a n = v 2 ρ

Logo, no ponto B ,

N B = v B 2 ρ = 51,57 1,5 = 34,38   N

Passo 3

Em seguida, vamos analisar os dados no Ponto C :

Aplicando o Princípio do Trabalho e Energia, temos

T 1 + ∑ U 1 - 2 = T 2

onde

T 1 = 1 2 m v A 2 = 1 2 1 9 2 = 40,5

T 2 = 1 2 m v C 2 = 1 2 ( 1 ) v C 2

∑ U 1 - 2 = - W y = - 1 9,81 3 = - 29,43

Substituindo esses valores na equação inicial, obtemos

40,5 - 29,43 = 0,5 v C 2

v C 2 = 22,14

v C = 4,705   m / s

Agora, utilizando a Equação do Movimento, temos

∑ F n = m a n

N C + W = m a C

N C + m g = ( 1 ) a C

Sabemos que

a n = v 2 ρ

Logo, no ponto C ,

N C + 1 9,81 = v C 2 ρ

N C = 4,95   N

Resposta

v B = 7,18   m / s

N B = 34,38   N

v C = 4,705   m / s

N C = 4,95   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade do cilindro de 8k g é de 0,3m / s em um determinado instante. Qual é a sua velocidade v após uma queda adicional de 1,5m ? A massa do tambor com o seu encaixe é de 12k g , seu raio de gir
A placa retangular uniforme tem uma massa de 300k g e é sustentada no plano vertical pelas duas hastes paralelas de massa desprezível e pelo cabo A C . Se o cabo se rompe de repente, determine a veloc
O caixote retangular homogêneo possui uma massa de 120k g e está sustentado na posição horizontal pelo cabo em A e pela dobradiça no canto O . Se o cabo em A é liberado repentinamente, calcule a veloc
Uma haste esbelta de comprimento l e massa m está soldada na borda de um aro de raio l . Se o aro é liberado a partir do repouso na posição mostrada, determine a velocidade v do centro do aro, após te
A polia com raio de 400m m tem uma massa de 50k g e um raio de giração de 300m m . A polia e sua carga de 100k g estão suspensas pelo cabo e pela mola, que possui uma rigidez de 1,5k N / m . Se o sist