Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 43
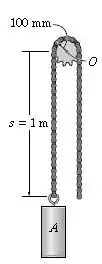
Resolva o Problema 18.42 supondo que a corrente tenha uma massa por unidade de comprimento de . Despreze, para o cálculo, a porção da corrente que está encaixada na engrenagem.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Podemos aplicar o princípio da conservação de energia analisando o momento incial e final do sistema.
A conservação de energia é dada por:
Vamos analisar cada componente:
Temos também que:
Como o sistema está em repouso no momento inicial, temos que e são nulos, logo:
Passo 2
Para o momento final, temos:
A parcela cinética final é dada por:
Onde:
Como , temos:
Passo 3
Vamos aplicar conservação de energia:
Resposta
Exercícios de Livros Relacionados
Se a superfície de contato entre o bloco de 20 kg e o solo é lisa, determine a potência de força F quando t = 4 s. Inicialmente, o bloco está em repouso.
Se F = 10 sN , onde s é dado em metros e a superfície de contato entre o bloco e o solo é lisa, determine a potência de força F quando s = 5 m. Inicialmente, o bloco de 20 kg está em repouso.
Se a carga de 50 kg A é içada pelo motor M de maneira que a carga tenha uma velocidade constante de 1,5 m/s, determine a potência de entrada do motor, o qual opera com uma eficiência de ϵ = 0,8 .
Se o motor recolhe o cabo com uma velocidade constante de v = 1 m/s, determine a potência fornecida ao motor. A carga pesa 500 N e a eficiência do motor é ϵ = 0,8 . Despreze a massa das polias.
O coeficiente de atrito cinétivo entre o bloco de 20 kg e o plano inclinado é μ k = 0,2 . Se o bloco está se deslocando para cima no plano inclinado com uma velocidade constante de v = 5m / s , determ