Exercícios de Energia Potencial - Lista de Exercícios Resolvida

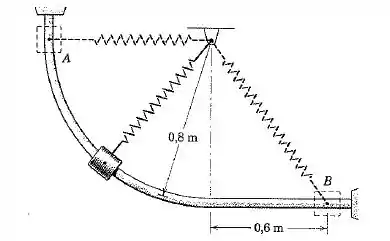
A mola tem um comprimento não esticado de e uma rigidez de . O Cursos de e a mola conectada são liberados a partir do repouso em e se deslocam no plano vertical. Calcule a velocidade do cursos quando este atinge na ausência de atrito.

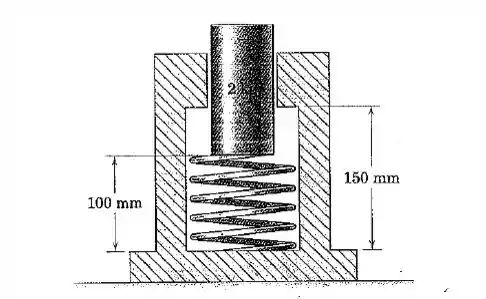
O êmbolo de é liberado a partir do repouso na posição mostrada onde a mola de rigidez foi comprimida para a metade do seu comprimento sem deformação de . Calcule a altura máxima acima da posição inicial alcançada pelo âmbolo.

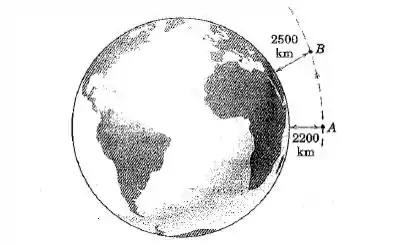
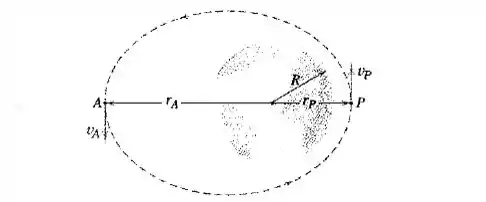
Um satélite artificial que se desoloca em uma órbita elíptica tem uma velocidade de a uma altitude de km no ponto . Determine sua velocidade no ponto onde a altitude é . Considere a Terra como uma esfera de raio e use para a aceleração da gravidade na superfície da Terra.

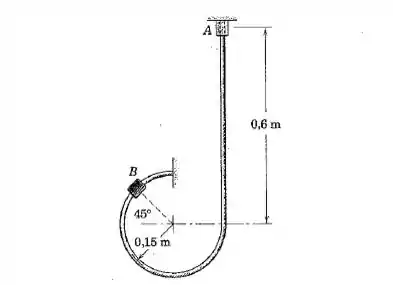
Um cursor com uma massa de é liberado a partir do repouso em e desliza para baixo e em torno do arame liso fixo. Determine a força entre o arame e o cursor quando este passa o ponto .

Um satélite é colocado em uma órbita elíptica em torno da Terra e tem uma velocidade na posição do perigeu . Determine a expressão para a velocidade na posição do apogeu . Os raios para e são, respectivamente, e . Observe que a energia total permanece constante.

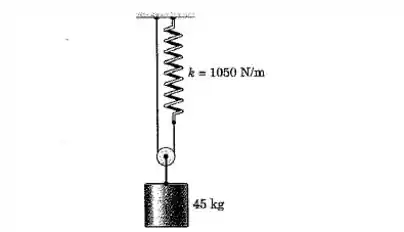
O sistema é liberado a partir do repouso com a mola inicialmente esticada em . Calcule a velocidade do cilindro após este ter caído . A mola tem uma rigidez de . Despreze a massa da pequena polia.

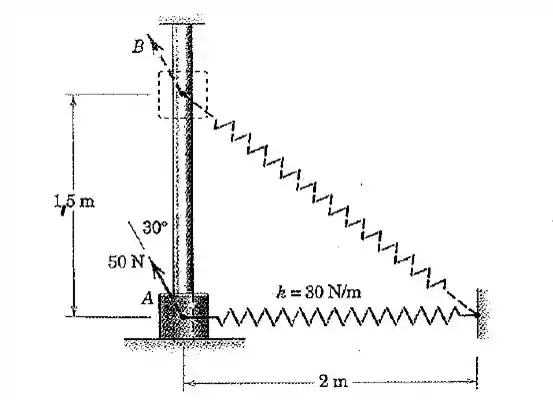
O cursor tem uma massa de e está preso à mola leve, que tem uma rigidez de e um comprimento sem deformação de . O cursor é liberado a partir do repouso em e desliza para cima na barra lisa sob a ação da força constante de . Calcule a velocidade do cursor quando este passa a posição .

03) Um disco homogêneo, de massa e raio , pode rolar sem escorregar sobre uma superfície plana horizontal que está fixa com respeito a um referencial inercial. A mola linear, de rigidez e comprimento natural , está vinculada a uma base fixa em e ao disco em seu centro . Seja o ângulo entre e a vertical , indicado na figura. Pede-se:

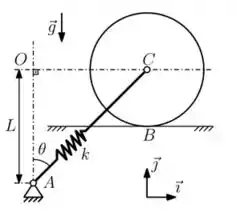
a) O diagrama de corpo livre para o disco.

b) As expressões, em termos de e , do vetor posição , da velocidade do ponto e da velocidade angular do disco.

c) A expressão da energia cinética do sistema.

d) A expressão da energia potencial do sistema.

e) Considerando que o sistema parta do repouso na configuração , determine o vetor de rotação do disco quando o sistema atingir pela primeira vez a configuração .

Dado: para o disco,