Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 51

Resolva o Problema 7.29 usando o círculo de Mohr.

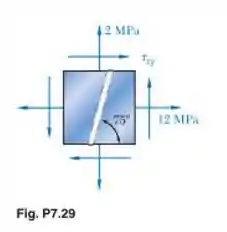
Passo 1

Tá legal! Nesse exercício nós vamos esboçar o círculo de Mohr para o estado de tensão dado e depois rotacionar o elemento de 75°, ou seja, percorrer 150° no círculo, para encontrar o plano desejado e fazer com que a tensão de cisalhamento seja zero nesse plano. Fazendo isso conseguimos encontrar a tensão de cisalhamento pedida na letra (a).

Depois, para a letra (b), vamos encontrar o raio do círculo, ainda com o auxílio do desenho feito para depois encontrar as tensões principais correspondentes.

Passo 2

Então vamos lá! Vamos começar escrevendo as tensões que temos de acordo com o elemento dado no enunciado, então teremos:

sigma_x = 12 M P a

sigma_y = 2 M P a

Para esboçar o círculo de Mohr, precisamos também da coordenada do centro, que é dada por:

C : ( sigma_m e d ; 0 )

E, sabemos que a tensão média é dada por:

sigma_m e d = (sigma_x + sigma_y)/(2) = (12 + 2)/(2) -> sigma_m e d = 7 M P a

Então as coordenadas para esboçar o círculo de Mohr serão:

X : (sigma_x ; - tau_x y) = (12 ; - tau_x y) M P a

Y : (sigma_y ; tau_x y) = (2 ; tau_x y) M P a

C : (sigma_m e d ; 0) = (7 ; 0) M P a

Com esses pontos, temos o seguinte círculo de Mohr:

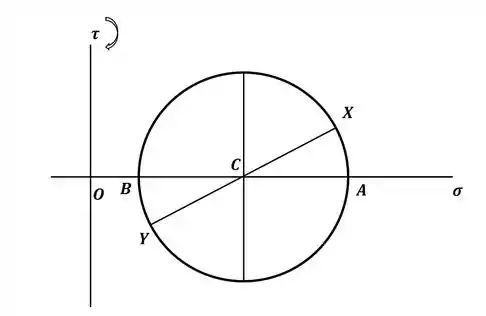
Passo 3

Beleza! Sabemos que o plano paralelo à solda fica a 75° no sentido anti-horário do plano dado, ou seja, precisamos andar 150° no círculo de Mohr. Fazendo isso, temos que ter tensão de cisalhamento zero, ou seja, devemos estar em cima do eixo “tensão” do círculo de Mohr, dessa forma, devemos ter a seguinte rotação no círculo:

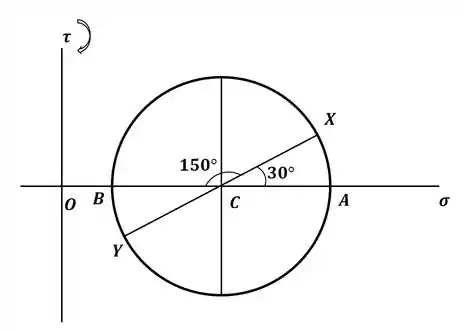
Então, podemos ver que o ponto X deverá ficar em cima do ponto B, onde temos tau = 0 . Dessa forma, a tensão de cisalhamento no estado dado pode ser encontrado através do ângulo de 30° formado no desenho e as tensões sigma_x e sigma_y que já foram dadas no enunciado:

t g 30 ° = - (tau_x y)/((sigma_x - sigma_y)/(2))

Isolando a tensão de cisalhamento e substituindo os valores conhecidos, teremos:

tau_x y = - (sigma_x - sigma_y)/(2) t g 30 ° = - (12 - 2)/(2) t g 30 °

tau_x y = - 2,89 M P a

A letra (a) já era! Bora pra (b).

Passo 4

Agora, para a letra (b), precisamos encontrar as tensões principais, que são dadas por:

sigma_1 = sigma_m e d + R

sigma_2 = sigma_m e d - R

Nós já temos o valor de sigma_m e d , que vimos lá no passo 2. Então precisamos calcular o valor do raio do círculo. Vamos fazer isso com o auxílio do círculo esboçado no passo 3, onde teremos:

s e n 30 ° = - (tau_x y)/(R)

Isolando o R dessa equação e substituindo o valor de tau_x y encontrado no passo 3, temos:

R = - (tau_x y)/(s e n 30 °) = - (- (2,89)/(0,5)) -> R = 5,77 M P a

Então, as tensões principais serão:

sigma_1 = sigma_m e d + R = 7 + 5,77 -> sigma_1 = 12,77 M P a

sigma_2 = sigma_m e d - R = 7 - 5,7 7 -> sigma_2 = 1,23 M P a

Proonto! Finalizamos mais um!

Resposta

(a) : tau_x y = - 2,89 M P a

(b) : sigma_1 = 12,77 M P a

(b) : sigma_2 = 1,23 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

71. Determine(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
69. Determine o estado de tensão equivalente se um elemento estiver orientado a 30 ° em sentido horário em relação ao elemento mostrado. Mostre o resultado no elemento.
73. Determine(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
74. Determine(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
72. Determine(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.