Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 52

Resolva o Problema 7.30 usando o círculo de Mohr.

Passo 1

Tá legal! Nesse exercício nós vamos esboçar o círculo de Mohr para o estado de tensão dado e depois explorar as duas possibilidades para os valores de , encontrando os comprimentos dos segmentos de reta que esboçamos, para encontrar o intervalo de valores admissíveis.

Passo 2

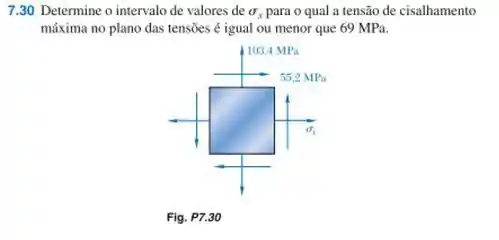
Então vamos lá! Vamos começar escrevendo as tensões que temos de acordo com o elemento dado no enunciado, então teremos:

Para esboçar o círculo de Mohr, precisamos também da coordenada do centro, que é dada por:

E, sabemos que a tensão média é dada por:

Não conseguimos calcular a tensão média ainda, pois não temos o valor de . Então as coordenadas para esboçar o círculo de Mohr serão:

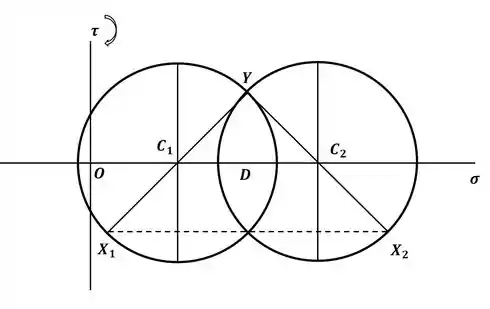
Com esses pontos, e levando em conta que podemos ter 2 valores extremos possíveis para , ou seja, para o ponto X, teremos duas configurações do círculo de Mohr, sendo assim, temos:

Passo 3

Beleza! Como foi dito no enunciado que a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 69 MPa, isso quer dizer que esse será o nosso raio limite do círculo de Mohr, independente da configuração de , então temos:

Então, com isso, conseguimos encontrar os dois comprimentos com relação ao centro e ao ponto Y do círculo de Mohr do passo 2, onde temos:

Agora, dos círculos esboçados no passo 2, podemos enxergar a seguinte relação trigonométrica:

Então, substituindo os valores conhecidos, temos:

Agora vamos sair encontrando as coordenadas de todos os pontos, para poder encontrar o intervalo admissível para . Sendo assim, as coordenadas do ponto são:

Da mesma forma, para o ponto , como teremos:

Agora, as coordenadas do ponto podem ser dadas por:

E, para o ponto , teremos:

Sendo assim, como vimos lá no passo 1 que as coordenadas do ponto X são dadas por:

O nosso intervalo de interesse para corresponde aos valores das coordenadas encontradas para e , então teremos:

É isso aí! Acabamos mais um!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16. As componentes do estado plano de deformação no ponto sobre a aba do pino são ϵ x = ( 200 × 10 - 6 ) , ϵ y = ( 180 × 10 - 6 ) e γ x y = ( - 300 × 10 - 6 ) . Use as equações de transformação da def

15. As componentes do estado plano de deformação no ponto da aba da bequilha são ϵ x = ( - 400 × 10 - 6 ) , ϵ y = ( 860 × 10 - 6 ) e γ x y = ( 375 × 10 - 6 ) . Use as equações de transformação da defo

Um extensômetro colocado no plano vertical sobre a superfície externa a um ângulo de 60 ° em relação ao eixo do tubo dá uma leitura ϵ A =-250 ( 10 - 6 ) no ponto A . Determine as deformações principai

63. Resolva o Problema 9.14 usando o círculo de Mohr.

66. Determine o estado de tensão equivalente se um elemento estiver orientado a 20 ° em sentido horário em relação ao elemento mostrado. Mostre o resultado no elemento.