Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 51
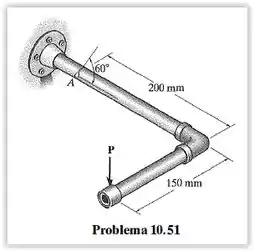
Um extensômetro colocado no plano vertical sobre a superfície externa a um ângulo de em relação ao eixo do tubo dá uma leitura no ponto . Determine as deformações principais no tubo no ponto . O tubo tem diâmetro externo de e diâmetro interno de e é feito de bronze .
Passo 1
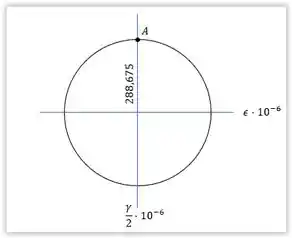
Vamos primeiro descobrir a deformação por cisalhamento . Para isso, podemos aplicar a equação de transformação da deformação para o ponto :
Passo 2
O segundo passo é calcular a deformação média . Usaremos a equação:
Como e são iguais a zero, temos que:
Portanto, a tensão de deformação normal média se encontra no centro do círculo de Mohr.
Passo 3
Para encontrar as deformações principais no tubo no ponto , podemos usar a equação:
Observe que o módulo do resultado de , , corresponde a medida do raio do círculo de Mohr.
