Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 15
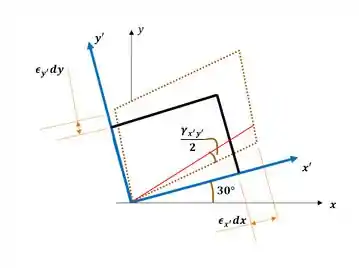
15. As componentes do estado plano de deformação no ponto da aba da bequilha são , e . Use as equações de transformação da deformação para determinar as deformações equivalentes no plano sobre um elemento orientado a um ângulo em sentido anti-horário em relação à posição original. Trace um esboço do elemento distorcido devido a essas deformações no plano . Utilize o círculo de Mohr.
Passo 1
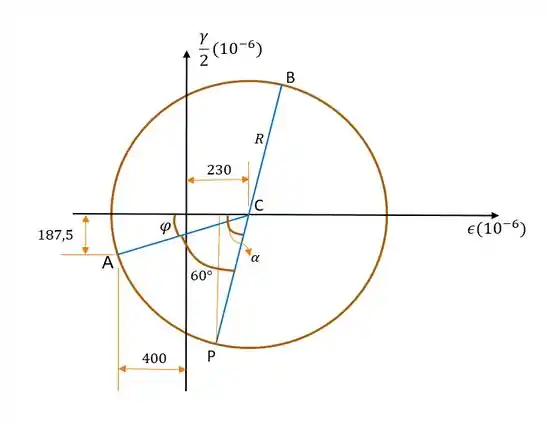
Vamos seguir passo a passos os procedimentos para construir o círculo de Mohr:
Calcularemos a deformação normal média que será o centro do círculo:
Passo 2
Agora devemos achar o raio do círculo:
Passo 3
Como já temos o raio e o centro do nosso círculo, já podemos construí-lo
Passo 4
O ângulo foi achado da seguinte maneira:
Passo 5
Agora, se você reparar bem a questão nos fornece que o elemento está orientado a um ângulo em sentido anti-horário em relação à posição original. Como no círculo de Mohr, trabalhamos com o dobro do ângulo em que o elemento está orientado , podemos achar o ângulo como:
Passo 6
Por meio do círculo, podemos calcular a deformação normal equivalente no eixo como:
Passo 7
De modo semelhante ao passo anterior, vamos calcular a deformação normal equivalente no eixo :
Passo 8
Finalmente, calcularemos a deformação por cisalhamento do nosso elemento como:
Passo 9
Como já obtemos nossas deformações, vamos fazer o esboço do nosso elemento, dado que ele está orientado a no sentido anti-horário. Ele vai ter, então, a seguinte cara:
