Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 127
Resolva o Problema considerando que .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Nos foi dito que:
E:
Para que a chave seja travada automaticamente, o atrito deve ser suficiente para manter o equilíbrio, pois o é aumentado de a , além de impedir o deslizamento da correia no tubo.
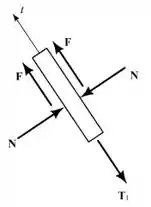
Sabendo disso, chegou a hora de desenharmos o diagrama de corpo livre do sistema:
Passo 2
A partir da geometria da figura, podemos calcular o valor de e . Temos que:
Sabemos que:
Portanto:
E:
Passo 3
Analisando o momento sobre o ponto , temos que:
Substituindo temos que:
Substituindo os valores conhecidos, temos que:
Resolvendo, teremos:
Passo 4
Fazendo a análise das forças em , temos que:
Quando houver escorregamento iminente, temos que:
Logo:
Portanto:
Podemos obter a relação:
Substituindo pelo valor encontrado anteriormente, temos que:
Portanto:
Passo 5
Agora temos que verificar o cinto no tubo. Vamos desenhar o diagrama do corpo livre de uma pequena porção da correia em sobre o eixo :
Temos que:
Temos que:
Transformando para , temos:
Passo 6
Quando o cinto está na iminência de escorregar, temos que:
Logo:
Substituindo os valores, temos que:
Temos que o maior valor de deve ser o considerado como valor limite para o qual a chave será travada