Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 31
Resolva os Problemas 7.5 e 7.9 usando o círculo de Mohr
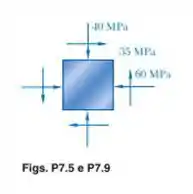
Passo 1
Beleza! Através do estado de tensões que foi dado no enunciado, conseguimos esboçar o círculo de Mohr para esse estado. A partir do círculo, podemos encontrar a inclinação dos planos principais e suas tensões.
Passo 2
Tá legal! Vamos começar escrevendo as tensões que temos para o nosso elemento diferencial, onde teremos:
Agora, calculando a tensão média, que é dada por:
Substituindo os valores conhecidos, teremos:
Agora, vamos escrever as coordenadas dos pontos para o círculo de Mohr, no nosso caso, temos:
Agora, sabemos que uma das direções principais será dada pela seguinte equação:
Agora, sabemos que a outra direção principal fica a 90° de rotação no elemento diferencial, ou seja, a 180° de rotação no círculo de Mohr, então a outra direção principal será:
Passo 3
Beleza, agora vamos para a letra (b) do exercício 7.5. Nesse caso, vamos calcular o raio do círculo através da fórmula que é dada por:
Substituindo os valores conhecidos, teremos:
Com isso podemos encontrar as tensões principais, que são dadas através de:
Beleza!! Fechamos o exercício 7.5. Vamos agora resolver o 7.9.
Passo 4
Agora podemos encontrar a inclinação dos planos de cisalhamento máximo pedido na letra (a), lembrando que eles estão sempre a 45° de inclinação com relação ao plano principal, teremos:
Substituindo os valores conhecidos, teremos:
Agora, para a letra (b) do exercício 7.9, nós sabemos que a tensão máxima de cisalhamento será o próprio raio do círculo de Mohr, ou seja:
E, sabemos que nesse ponto, estamos no centro do círculo, então a nossa tensão normal correspondente é igual a tensão média, então teremos: