Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 107b
Resolver o , assumindo que uma única força de é aplicada no ponto C.
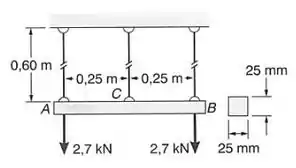
Passo 1
Já temos a primeira equação, a segunda é muito simples, basta fazermos um somatório de momentos no ponto B e assim teremos a segunda equação do nosso sistema, que poderemos determinar usando nossa viga como referência.
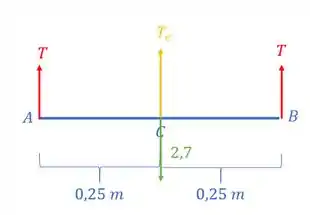
Assim, temos as seguintes duas equações:
Substituindo, tem-se que:
E assim determinamos as trações nos pontos A e B, no ponto C vai ser dado por:
Resposta
Exercícios de Livros Relacionados
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Para P = 360k N , determinar:A reação em BA declividade em BA deflexão em AUsar E = 200G P a
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Para P = 360k N , determinar:A reação em BA declividade em BA deflexão em AUsar E = 200G P a
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Sabendo-se que E = 200G P a , determinar:a intensidade P da carga para que a declividade em A seja zero.A co
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Sabendo-se que E = 200G P a , determinar:a intensidade P da carga para que a declividade em A seja zero.A co
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Sabendo-se que E = 200G P a , determinar:a intensidade P da carga para que a deflexão em A seja zero.A corre