Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 179
Sabendo-se que a tensão admissível de compressão é , determinar a maior distância permissível da linha de ação da força de , ao plano que contém o centro de curvatura da barra.
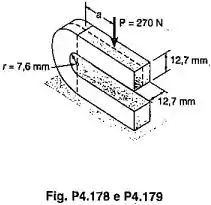
Passo 1
A região que sofre maior esforço é o centro da curva. Então vamos fazer uma seção neste ponto e calcular os esforços internos
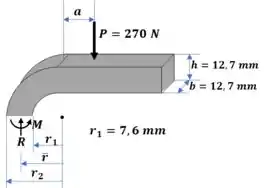
Primeiro vamos calcular as propriedades geométricas da seção: raio do centroide, raio externo e área:
Passo 2
Com o raio podemos calcular o momento interno, já que a distância entre a força e o centro da viga é
E a carga interna será igual a carga
Passo 3
Como a seção é quadrada, a gente calcula o raio da linha neutra pela equação:
E com isso, a gente calcula a excentricidade:
Passo 4
Cuidado! Um erro comum nesse tipo de questão é esquecer de calcular a tensão gerada pela força interna R:
Não esqueça de que é uma compressão! Ou seja, a tensão é negativa:
Passo 5
Como a tensão é uma compressão, então podemos assumir que a maior tensão ocorrerá em quando a compressão for a maior possível, ou seja, quando . Aplicando:
Usando um pouco de matemágica, vamos isolar o
E aplicamos os valores: