Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 43
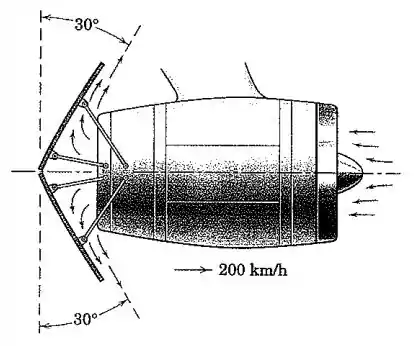
Um reversor de empuxo de um motor a jato para reduzir a velocidade de uma aeronave com após a aterrissagem emprega pás dobradiças que desviam os gases de escape na direção indicada. Se o motor está consumindo de ar e de combustível por segundo, calcule o empuxo de frenagem como uma fração do empuxo motor sem as pás defletoras. Os gases de escape têm uma velocidade de em relação ao bocal.
Passo 1
Quando as pás defletoras estão na posição da figura, há escoamento de ar e combustível numa taxa:
saindo da aeronave a uma velocidade horizontal em relação ao bocal:
Por outro lado, há entrada de ar a uma taxa e a uma velocidade .
Passo 2
Agora, lembre-se de que a variação na quantidade de movimento horizontal do sistema será:
Como , o empuxo de frenagem será justamente:
Passo 3
Se não tivermos as pás refletoras, as correntes de massa entrarão e sairão da aeronave com velocidade para a esquerda, de modo que:
Então, calculamos o empuxo motor :
Logo,