Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 35
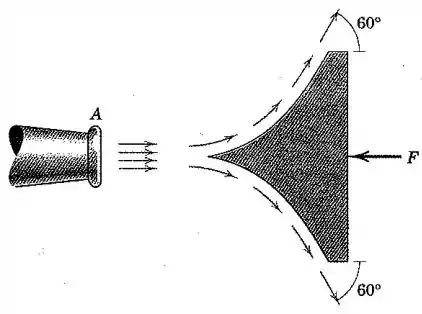
A água doce escoa do bocal com uma velocidade de na taxa de e é dividida em duas correntes iguais pela pá fixa e desviada a como mostrado. Calcule a força necessária para manter a pá no lugar. A massa específica da água é .
Passo 1
A taxa de escoamento é dada por:
Logo, o equilíbrio de forças na direção (mesma direção da velocidade de escoamento) nos dá a seguinte equação:
Pelo fato de as correntes estarem descendo ou subindo uma inclinação de , teremos:
Resposta
Exercícios de Livros Relacionados
O carro de 2 M g está sendo rebocado por um guincho. Se o guincho exerce uma força T = 100 sN sobre o cabo, onde s é o deslocamento do carro em metros. Determine a velocidade escalar do carro quando s
Uma mola de rigidez k = 500 N m está montada contra o bloco de 10k g . Se obloco está sujeito à força F = 500N , determine a sua velocidade em s = 0,5m . Quando s = 0, o bloco está em repouso e a mola
O motor enrola o cabo com uma acelareção constante de tal maneira que a caixa de 20 kg se move em uma distância s = 6 m em 3 s, partindo do repouso. Determine a tração desenvolvida no cabo. O coeficie
A caminhonete de 2 Mg está se movendo A 15 m∕s quando os freios em todas suas rodas são aplicados, fazendo com que ele escorregue por uma distância de 10 m antes de chegar ao repolso. Determine a forç
O trem de 160 Mg parte do repolso e começa a subir o aclive, como mostrado. Se o motor exerce uma força de tração F de 1 ∕ 8 do peso do trem, determine a velocidade do trem quando ele tiver avançado u