Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 41
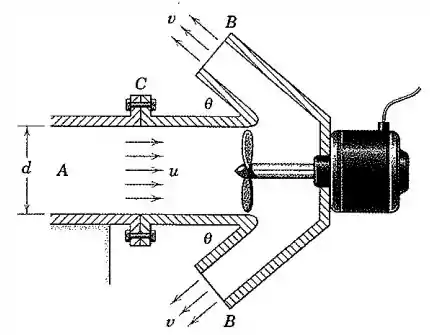
A bomba mostrada aspira ar com uma massa específica através do duto fixo com diâmetro a uma velocidade e o descarrega em alta velocidade através das duas saídas . A pressão nos fluxos de ar em e é a atmosférica. Determine a expressão para a tração exercida sobre a unidade de bombeamento através do flange em .
Passo 1
Se considerarmos a direção como a direção da velocidade , veremos que existe uma alteração da quantidade de movimento do sistema nessa direção, já que a massa de ar entra com velocidade e sai com velocidade (componente na direção de ). Então, isso gera uma tração para a esquerda, de modo que:
Para calcular a taxa de escoamento , fazemos assim:
Passo 2
Como já vimos, a variação de velocidade em será:
Então:
Resposta
Exercícios de Livros Relacionados
Para os vetores V → 1 e V → 2 dados, determine V 1 + V 2 , V → 1 + V → 2 , V 1 → - V → 2 , V 1 → × V 2 → , V 2 → × V 1 → e V 1 → ∙ V 2 → . Considere que os vetores sejam adimensionais.
A que altitude h acima do pólo norte o peso de um objeto é reduzido para 10 % do seu valor na superfície terrestre? Assuma a Terra esférica com raio R e expresse h em termos de R .
Determine a razão R A da força exercida pelo Sol sobre a Lua por aquela exercida pela Terra sobre a Lua para a posição A da Lua. Repita para Lua na posição B .
As três esferas com 100m m de diâmetro constrúidas com diferentes metais estão localizadas nos vértices de um triângulo equilátero no espaço profundo. Determine a resultante R das forças gravitacionai
O rebocador de combate a incêndio despeja um jato de água salgada (massa específica 1030k g / m 3 ) com uma velocidade em relação ao bocal de 40m / s na taxa de 0,080m 3 / s . Calcule o empuxo propuls