Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 169
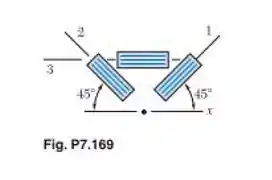
Determine a maior deformação específica normal no plano das deformações, sabendo que foram obtidas as seguintes deformações específicas usando a roseta abaixo:
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o conjunto de equações 7.60, dado por:
Vamos substituir os valores conhecidos para cada um dos 3 casos descritos, chegando num sistema de equações, depois disso temos que resolver o sistema. Com o sistema resolvido fica fácil, temos as deformações para calcular a deformação média e o raio do círculo de Mohr, com essas informações conseguimos calcular a deformação máxima, que é dada por:
Então bora lá!
Passo 2
Tá legal! Vamos começar escrevendo os ângulos que nós temos:
Então beleza! Vamos substituir os valores conhecidos na primeira equação, chegando em:
Essa será nossa equação 1. Agora vamos substituir os valores conhecidos na segunda equação, chegando em:
Essa será nossa equação 2. E agora, substituindo os valores conhecidos na terceira equação, chegamos em:
Opa! Já conseguimos o valor de
Passo 3
Agora nós vamos somar as equações 1 e 2 que obtemos no passo 2, chegando em:
Substituindo o valor de obtido no passo 2, conseguimos obter o valor de :
E, substituindo esse valor e o valor para na equação 1, podemos encontrar o valor de , que será:
Beleza, com as deformações no plano, podemos calcular a deformação média, que será:
E agora, podemos calcular o raio do círculo de Mohr, que é dado por:
Então, a maior deformação específica normal no plano das deformações será:
Shooow! Fechamos mais um exercício, valeeu!