Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 91
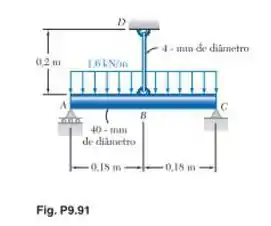
Sabendo que a haste ABC e o cabo BD são feitos de aço, determine (a) a deflexão em B, (b) a reação em A. Utilize E = 200 GPa.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o princípio da superposição para encontrar cada uma das inclinações e deflexões e depois somar para encontrar uma expressão para a deflexão total em B. Depois disso será possível encontrar a reação em A.
Passo 2
Tá legal! Vamos começar esse exercício encontrando o momento de inércia da nossa viga, como temos uma seção circular, o momento de inércia:
Vamos aproveitar e calcular o valor do termo EI, que também usaremos lá na frente. Então teremos:
Tá legal, a primeira coisa que vamos escrever é o alongamento causado no cabo de aço BD, devido ao carregamento aplicado na haste. Esse alongamento será dado por:
Em que é o comprimento do cabo, é a força aplicada nele, E é o modulo de elasticidade e A é a seção transversal do cabo. Beleza, vamos deixar essa equação guardada por enquanto. Como vamos precisar depois, já vamos calcular a área da seção transversal do cabo de aço, que será dada por:
Passo 3
Agora nós vamos separar o carregamento aplicado na viga, pois temos a força localizada que o cabo exerce sobre a viga e o carregamento distribuído. Então, para o primeiro caso, onde teremos somente a força localizada, temos o seguinte DCL:
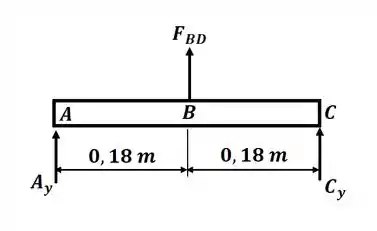
Agora podemos utilizar o apêndice D para pegar a deflexão no ponto B, nesse caso temos o caso 4 do apêndice D, onde teremos:
Agora para o segundo caso, onde temos um carregamento distribuído ao longo de toda a viga, teremos que a deflexão no ponto B será dada pelo caso 6 do apêndice D, onde teremos:
Beleza! Agora sabemos que a deflexão no ponto B causada pelos carregamentos aplicados na viga tem que ser igual a deflexão sofrida pelo cabo de aço, só mudando o sentido da deflexão. Então, somando as duas deflexões obtidas pelos carregamentos e igualando com a deflexão do cabo de aço encontrada, teremos:
Substituindo as expressões encontradas, teremos:
Isolando o termo e substituindo os valores conhecidos, teremos:
Então, a deflexão em B pode ser encontrada através do alongamento do cabo de aço, onde temos:
Beleza! A letra (a) já era, bora pra (b) agora.
Passo 4
Agora, para encontrar a reação no apoio A, basta fazer um equilíbrio de forças para o sistema. No nosso caso, como o carregamento é simétrico, teremos a mesma reação nos pontos A e C, sendo a metade da força total aplicada na viga. Então teremos:
Substituindo os valores conhecidos, teremos:
Shoow! Terminamos mais um, valeeu!