Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 175

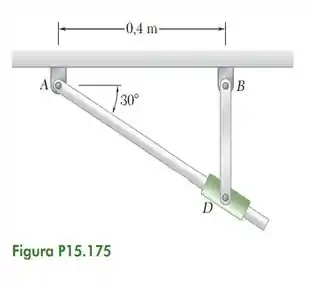
Sabendo que, no instante mostrado na figura, a barra articulada em B gira no sentido anti-horário com velocidade angular constante ω B de 6 rad /s, determine a velocidade angular e a aceleração angular da barra articulada em A.

Passo 1

O enunciado pede que a gente determine a velocidade angular e a aceleração angular da barra articulada em A

Pois muito bem! Vamos começar! Do enunciado e da figura disponível nele, conseguimos extrair os seguintes dados...

A B = 0,4   m

B D = 0,4 tan ⁡ 30 °   m

A D = 0,4 cos ⁡ 30 °   m = 0,4 sec ⁡ 30 °   m

Agora se liga! Pegando o pino A , que está fixo, como referência, temos que...

Ω = ω A

E com isso, temos que a velocidade do ponto coincidente D em relação à A, será dada por...

v D ' = A D ω A = 0,4 ω A sec ⁡ 30 °   ⦨ 60 °

E também temos que...

a D ' = A D α A   ⦨ 60 ° + A D ω A 2   ⦩ 30 °

a D ' = 0,4 sec ⁡ 30 ° α A   ⦨ 60 ° + 0,4 sec ⁡ 30 ° ω A 2   ⦩ 30 °

Passo 2

Continuando nossa raciocínio, chamando de v D / F a velocidade do colar D relativo ao plano, temos que...

v D / F = u   ⦪ 30 °

E a aceleração será de...

a D / F = u ˙   ⦪ 30 °

Consequentemente, temos que a aceleração de Coriolis valerá...

2 ω A u   ⦨ 60 °

Assim, a velocidade em D , v D será de...

v D = v D ' + v D / F

v D = 0,4 ω A sec ⁡ 30 ° ⦨ 60 ° + [ u   ⦪ 30 ° ]

E consequentemente, a aceleração em D valerá...

a D = a D ' + a D / F + 2 ω A u   ⦨ 60 °

a D = 0,4 sec ⁡ 30 ° α A   ⦨ 60 ° + 0,4 sec ⁡ 30 ° ω A 2   ⦩ 30 ° + u ˙   ⦪ 30 ° + [ 2 ω A u   ⦨ 60 ° ]

Passo 3

Agora, vamos analisar a parte B D ! Temos que...

v D = B D ω B

v D = 0,4 tan ⁡ 30 ° ( 6 )

v D = [ 2,4 tan ⁡ 30 °   m / s ]   →

E baseado nisso, podemos escrever a aceleração em D , também como...

a D = B D ω B 2

a D = 0,4 tan ⁡ 30 ° ( 6 2 )

a D = [ 14,4 tan ⁡ 30 °   m / s 2   ↑ ]

Agora é uma questão de igualar as componentes para v D e resolver...

⦨ 60 ° ⇒ 0,4 sec ⁡ 30 ° ω A = 2,4 tan ⁡ 30 ° cos ⁡ 60 °

ω A = 1,5   r a d / s   ⤻

⦪ 30 ° ⇒ u = 2,4 tan ⁡ 30 ° cos ⁡ 30 °

u = 1,2   m / s

Fazendo o mesmo para com a D , temos que...

⦨ 60 ° : 0,4 sec ⁡ 30 ° α A + 2 ω A u = 14,4 tan ⁡ 30 ° sen ⁡ 60 °

Isolando α A :

α A = 14,4 tan ⁡ 30 ° sen ⁡ 60 ° - 2 ω A u 0,4 sec ⁡ 30 °

α A = 14,4 tan ⁡ 30 ° sen ⁡ 60 ° - 2 ⋅ 1,5 ⋅ 1,2 0,4 sec ⁡ 30 °

α A = 7,79   r a d / s 2   ⤿

Resposta

ω A = 1,5   r a d / s   ⤻

a A = 7,79   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 15.222, considerando que, no instante mostrado, a velocidade angular ω 1 da placa de 10r a d / s está decrescendo a uma taxa de 25r a d / s 2 , enquanto a velocidade relativa u do p
Usando o método da Seção 15.14 , resolva o Problema 15.19 2 .
Uma placa quadrada com 500m m de lado está articulada nos pontos A e B de um grampo em U . A placa gira à taxa constante ω 2 = 4r a d / s em relação ao grampo, que, por sua vez, gira à taxa constante
Um disco com raio de 120m m gira à taxa constante ω 2 = 5r a d / s em relação ao braço A B , que, por sua vez, gira à taxa constante ω 1 = 3r a d / s . Para a posição mostrada na figura, determine a v
A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos