Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 228
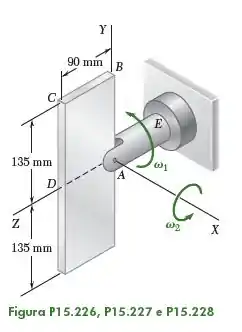
A placa retangular mostrada na figura gira à taxa constante em relação ao braço , que, por sua vez, gira à taxa constante em torno do eixo . Para a posição mostrada, determine a velocidade e a aceleração do ponto da placa indicado.
Canto .
Passo 1
Este exercício nos pede a velocidade e aceleração de Vamos organizar nossos dados do enunciado. Temos que:
O vetor posição com relação a é dado por:
Temos também que:
Sabemos que a velocidade escalar do ponto é dada por:
Onde:
Vamos aos cálculos.
Passo 2
Temos que:
A velocidade relativa entre e pode ser representada na forma vetorial:
Logo, a velocidade escalar do ponto será:
Passo 3
Para a aceleração do ponto , temos que:
Temos que:
Portanto:
Temos também que:
Logo:
Passo 4
Portanto:
Resolvendo, temos que
Resposta
Exercícios de Livros Relacionados
15.137. Representando por rA o vetor de posição do ponto A de uma placa rígida que está em movimento plano, mostre que (a) o vetor de posição rC do centro instantâneo de rotação é r C = r A + ω × v A
15.139. As rodas fixadas às extremidades da barra AB rolam ao longo das superfícies mostradas na figura. Usando o método da Seção 15.9 e sabendo que a aceleração da roda B é zero, deduza uma expressão
15.139. As rodas fixadas às extremidades da barra AB rolam ao longo das superfícies mostradas na figura. Usando o método da Seção 15.9 e sabendo que a aceleração da roda B é zero, deduza uma expressão
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s2, ambas orientadas para ci
Um tambor de 75 mm de raio está preso rigidamente a um tambor de 125 mm de raio, como mostra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do