Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 235
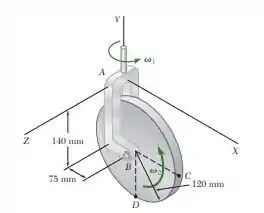
Um disco com raio de gira à taxa constante em relação ao braço , que, por sua vez, gira à taxa constante . Para a posição mostrada na figura, determine a velocidade e a aceleração do ponto .
Passo 1
Falaaaai meus amores, cêis tão baunzinho??
Bora resolver mais um comigooo, simboráa, moçadinha...
Para usarmos a velocidade de C, vamos usar a velocidade:
Vamos iniciar calculando o valor de
Passo 2
Agora iremos calcular o valor de
Logo, a velocidade escalar do ponto será:
Passo 3
Para a aceleração do ponto , temos que:
Primeiramente iremos calcular o valor de
Agora iremos calcular o valor de
Passo 4
Vamos fazer algumas substituições, logo:
Resposta
Exercícios de Livros Relacionados
Um carro C é suportado por um rodízio A e um cilindro B, cada um com 50 mm de diâmetro. Sabendo que no instante mostrado na figura o carro tem uma aceleração de 2,4 m/s² e uma velocidade de 1,5 m/s, a
Um automóvel desloca-se para a esquerda a uma velocidade constante de 80 km/h. Sabendo que o diâmetro da roda é de 500 mm, determine a aceleração (a) do ponto B, (b) do ponto C, (c) do ponto D.
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s², ambas orientadas para ci
A barra BDE está presa a duas hastes AB e CD. Sabendo que, no instante mostrado na figura, a haste AB gira com uma velocidade angular constante de 3 rad/s no sentido horário, determine a aceleração (a
15.140. O disco de acionamento do mecanismo de cruzeta escocesa mostrado na figura tem uma velocidade angular ω e uma aceleração angular α , ambas no sentido anti-horário. Usando o método da Seção 15.