Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 158
Sabendo que a intensidade da carga concentrada é , (a) trace os diagramas de esforço cortante e o momento fletor para a viga , (b) determine o máximo valor absoluto do esforço cortante e momento fletor.
Passo 1
Bom galera, vamos começar calculando as forças de reação e , sabendo que a viga encontra-se em equilíbrio e por simetria :
Passo 2
Show de bola, assim, o nosso diagrama de esforço cortante fica:
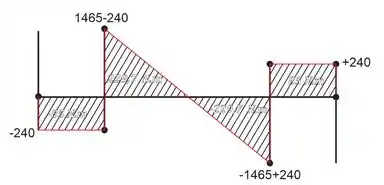
O máximo esforço cortante é:
Passo 3
Calma, tá quase acabando. Agora, o diagrama do momento fletor: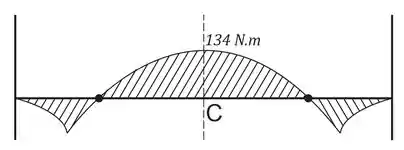
Então, a gente vê que o momento fletor máximo é:
Resposta
Exercícios de Livros Relacionados
Se o peso da viga é de W = 3 k N e o valor do ângulo dos cabos é θ = 30 . Trace os diagramas de cortante e momento fletor e (a) determine os esforços máximos absolutos.
Trace os diagramas de cortante e momento fletor e determine os valores máximos absolutos dos esforços na estrutura a seguir.
Para a figura do problema 7.43, determine (a) o valor de a para que o momento máximo seja o menor possível(b) o valor correspondente a M m á x . á (Use a dica do problema 7.55)
Trace os diagramas de cortante e momento fletor e determine os valores máximos absolutos dos esforços na estrutura a seguir.
Se o peso da viga é de W = 3 k N e o valor do ângulo dos cabos é θ = 60 . Trace os diagramas de cortante e momento fletor e (a) determine os esforços máximos absolutos.