Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 25

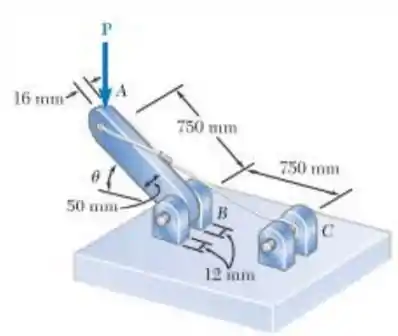
Sabendo que Ø=40 ° e P= 9 kN, determine (a) o menor diâmetro admissível do pino em B considerando que a tensão de cisalhamento média no pino não exceder 120 MPa, (b) a tensão de contato média no elemento AB em B, (c) a correspondente tensão de contato média em cada um dos suportes em B

Passo 1

  1. E aí gurizada tudo belezinha??? Antes de mais nada vamos desenhar o diagrama de corpo livre para facilitar os cálculos?

σ = F A  

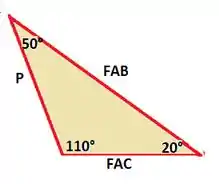
Decompondo as forças por Pitágoras temos:

P s e n   2 0 = F A B s e n   11 0 = F A C s e n 5 0

Agora temos que isolar “FAB”

F A B = P   s e n   11 0 s e n   2 0  

F A B = 9   s e n   110 s e n   20   = 24,72   × 10 3   N

Passo 2

  1. Para calcularmos a tensão de contato em AB em A

    2. σ = F A   = F t d

    σ = 24,72   × 10 3 / ( 0,016 × 11,45   × 10 - 3 )  

    σ = 135   M P a

    Isolando “d” temos:

    d 2 = 2 F A B π τ = 2 × 24,72   × 10 3 π × ( 120 × 10 6 )

    d = 11,453 × 10 - 3   m

    Passo 2

  2. Para calcularmos a tensão de contato em AB em A

    3. σ = F A   = F t d

    σ = 24,72   × 10 3 / ( 0,016 × 11,45   × 10 - 3 )  

    σ = 135   M P a

    Passo 3

  3. Tensão de contato nos suportes de suporte em B.

σ = F A   = F / 2 t d

σ = 24,72   × 10 3 / 2 / ( 0,012 × 11,45   × 10 - 3 )  

σ = 90   M P a

Resposta

  1. d = 11,453 × 10 - 3   m
  2. σ = 135   M P a
  3. σ = 90   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O arganéu da âncora suporta uma força de cabo de 3 kN. Se o pino tiver diâmetro de 6 mm, determine a tensão média de cisalhamento no pino.
A alavanca está presa ao eixo fixo por um pino cônico AB, cujo diâmetro médio é 6 mm. Se um binário for aplicado à alavanca, determine a tensão de cisalhamento média no pino entre ele e a alavanca.
A lâmpada de engate do vagão ferroviário é sustentada pelo pino de 3m m de diâmetro em A . Se a lâmpada pesar 20N e o peso do braço extensor A B for 8N / m , determine a tensão de cisalhamento média n
Resolva o problema 1.61 para o pino B , qual está sujeito a cisalhamento duplo e tem 5 m m de diâmetro.
O alicate de pressão é usado para dobrar a extremidade do arame E . Se uma força de 100N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino emA . O pino está sujeito