Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 63
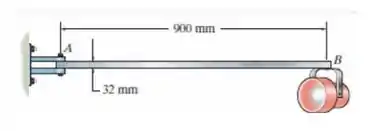
A lâmpada de engate do vagão ferroviário é sustentada pelo pino de de diâmetro em . Se a lâmpada pesar e o peso do braço extensor for , determine a tensão de cisalhamento média no pino necessária para sustentar a lâmpada. Dica: A força de cisalhamento no pino é causada pelo binário exigido para o equilíbrio em
Passo 1
Oláaa, querido! Tá bem? Ele quer a tensão de cisalhamento no pino para que essa estrutura com a lâmpada fique paradinha.
Primeiramente devemos lembrar como se calcula a tensão de cisalhamento que é dada por
onde
força interna de cisalhamento no pino;
: área do pino o ponto ;
Então para ter a tensão, a gente precisa saber a força de cisalhamento que atua no pino. E para achar o valor de uma força, é sempre maneiro fazer o diagrama de corpo livre da estrutura:
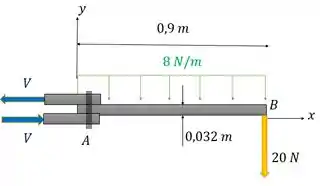
Aí essa carga distribuída é o peso do braço extensor (já que ele é dado em ), a carga de é o peso da lâmpada.
E o binário de é quem causa o momento necessário para o extensor não girar e cair. Essas forças de são aplicadas pela parede sobre essas pecinhas que se prendem ao pino.
Bora começar achando esse !
Passo 2
Para usar as equações de equilíbrio é bom passar essa carga distribuída para uma força concentrada equivalente. A força equivalente tem o valor da área do retângulo que representa a carga distribuída:
E ela fica na metade do braço extensor, então nosso diagrama mais simples é
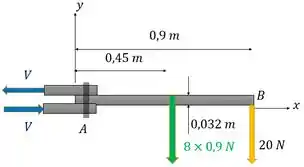
Aí para achar a gente pode calcular o momento em . Por que? Porque temos um binário formado pelo par de forças , que causa um momento na estrutura de , já que um binário é dado pelo produto do módulo de uma força e a distância entre as forças.
Então basicamente, nossa estrutura é assim:
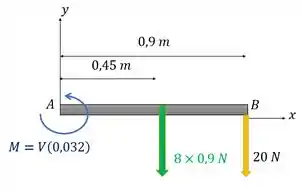
Dessa forma, adotando o sentido anti-horário como positivo vamos obter
Isolando :
Passo 3
Então a gente acabou de achar . E queremos a tensão de cisalhamento. Mas antes de calcular essa tensão, precisamos ver o cisalhamento que a gente tem é duplo ou simples. Vamos olhar nosso pino mais de perto. Dar aquele zoom esperto:
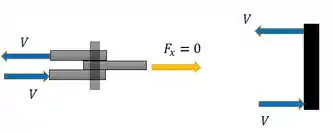
Percebe que esse par de foras se cancelam, então a gente não tem uma força horizontal no braço extensor. Isso significa que apenas temos o par de força atuando no pino.
Vamos fazer uma seção nele para achar a força de cisalhamento interna
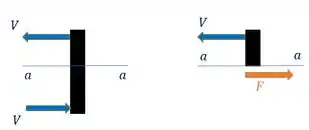
Percebe que a força de cisalhamento interna vai ser, pelo equilíbrio desse pino cortado,
Ou seja, temos um cisalhamento simples. E a tensão de cisalhamento vai ser
Passo 4
Nosso problema está quase terminando, resta-nos calcular a área da seção de cisalhamento que é a área do pino com seção circular
Assim, teremos que a tensão de cisalhamento média será dada por:
Lembrando que teremos