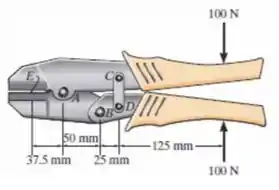
O alicate de pressão é usado para dobrar a extremidade do arame . Se uma força de for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em. O pino está sujeito a cisalhamento duplo e tem diâmetro de . Somente uma força vertical é exercida no arame.
Passo 1
Fala aí meu povo, como é que vocês estão? Todos prontos pra mais uma questãozinha maneira?

Como dizem por aí: “A voz do povo é a voz de Deus”, então, vamos para a nossa questão.
Como essa questão pede para que calculemos a tensão de cisalhamento médio no pino, vamos lembrar como é que se calcula essa bendita tensão, né?! A referida tensão é calculada através da fórmula:
onde
força vertical exercida sobre o pino;
: área do pino em
Como a gente já tem o diâmetro do pino que nos foi dado , a área vai ser de boas de encontrar, então o nosso foco vai ser encontrar a força no pino, ok? Bora lá!
Passo 2
Para achar a força no pino, vamos desenhar o nosso diagrama de corpo livre da chave.
Mas calma aí, essa chave tem vários pinos. Isso diz para gente que esse alicate é uma estrutura composta.
Como temos uma estrutura composta e ligada por pinos, uma forma de resolver é separar ela em mais de um elemento. E onde a gente faz a separação? Onde temos pinos!
Podemos olhar só para a metade de baixo do alicate, e soltar os pinos e . Fazendo um diagrama de corpo livre de cada elemento que forma a parte de baixo do alicate:
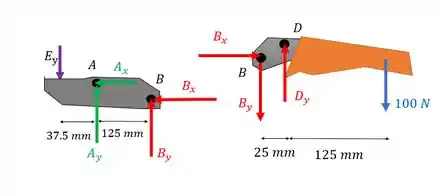
E por que gente escolhe só a metade de baixo? Porque na metade de cima só temos uma parte, e temos forças verticais desconhecidas em , e . Ou seja, não vamos conseguir achar através desse elemento porque não há equações de equilíbrio suficientes.
No máximo, podemos ter duas forças verticais desconhecidas, aí podemos usar o equilíbrio de momento para eliminar uma delas e achar a outra.
Já olhando na parte de baixo e dividindo essa parte soltando os pinos, vemos que o elemento da direita tem apenas duas forças verticais desconhecidas, então dá para resolver essa peça, e assim ter informação suficiente para achar as forças em pelo outro elemento.
E repara também que as forças que aparecem nos dois diagramas aparecem em sentidos opostos. Aí a ideia é então a gente usar o DCL da direita para achar as forças em , e com essa informação, achar as forças em pelo DCL da esquerda. Bora!
Passo 3
Vamos começar achando e no elemento que tem o pino , para então a gente poder resolver o elemento que tem o pino .
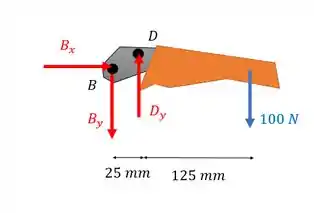
Fazendo o somatório dos esforços horizontais:
Temos:
Tomando, agora, o momento em e considerando o sentido anti-horário como positivo vamos ter:
Substituindo temos.
Passo 4
Beleza, agora vamos olhar a nossa outra parte do alicate, ok? Aí a gente consegue achar as tão desejadas forças atuando no pino onde a gente quer a tensão. Lembra que essa parte a gente achou soltando a peça que possui ligação em A e B, como na figura.
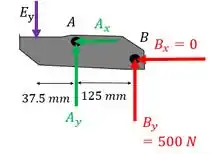
Repara que no ponto , vai haver apenas reação na vertical, de acordo com o que foi dito no enunciado!
De forma análoga ao que fizemos no diagrama anterior, vamos fazer aqui, começando pelas reações horizontais:
Para o momento, nesse caso, vamos utilizar como referência não mais o ponto e sim o ponto e vamos considerar o sentido anti-horário positivo.
Prontinho, achamos a força que atua no nosso querido pino 😊
Passo 5
Nesse ponto do problema estamos quase terminando nosso exercício. Boa, então falta só colocar a resposta aqui?

Lembrando que no enunciado foi dito que o pino sofre cisalhamento duplo, isso é, essa força que achamos é aplicada nele através das duas fazes do alicate. Ou seja, uma face é responsável por aplicar uma força de . E aí o cisalhamento é calculado pelo valor dessa força:
Agora uma última continha antes de só substituirmos tudo na formula da tensão de cisalhamento é calcular a área do nosso pino e como temos uma área que é uma circunferência sua área será dada por
Finalmente chegamos ao momento de alegria, onde vamos precisar apenas substituir tudo na fórmula da tensão de cisalhamento média de modo que obtemos
Dica: quando a gente divide por o resultado sai em . 😉 Saber isso por agilizar suas continhas!