Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 94
Sabendo que a tensão máxima do cabo é , determine a distância , a distância .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos o seguir o diagrama de corpo livre:
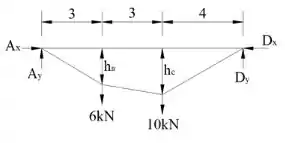
A forças de reação são determinadas usando as equações de equilíbrio:
Analisando as forças em , temos:
Calculando o momento no ponto , temos:
Desta análise também podemos encontrar a reação vertical em :
Passo 2
Fazendo o somatório de forças em podemos determinar o ângulo , como mostrado a seguir:
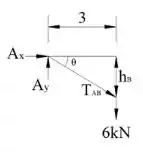
A altura será:
Passo 3
Para encontrar a altura primeiro temos que determinar . Os cálculos de e são mostrados a seguir:
Portanto:
Passo 4
Com o diagrama de força da seção , podemos determinar o valor da altura .
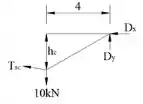
Calculando o momento no ponto , temos:
Resposta
Exercícios de Livros Relacionados
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localizaão do momento fletor máximo.
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localização do máximo valor absoluto do momento fletor.
Resolva o Problema 7.81 , considerando que a força aplicada de 4.500N em D é direcionada para cima.
Para a viga e carregamento mostrados na figura, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e localização do máximo valor absoluto do momento fletor.
Resolva o Problema 7.83 considerando que o momento de 20k N ⋅ m aplicado em B é no sentido anti-horário.