Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 78

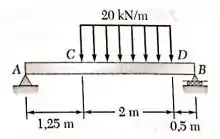
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localizaão do momento fletor máximo.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Desenhe o diagrama de corpo livre do sistema:

Esta carga distribuída gera uma carga pontual fictícia, localizada na metade de seu comprimento total e pode ser calculada por:

F R = q ⋅ L

F R = 20 2

F R = 40   k N

Podendo então ser representada assim:

Passo 2

Vamos fazer o somatório dos momentos no ponto B :

↶ + ∑ M B = 0

40 ( 1 , 5 ) - A y ( 3 , 75 ) = 0

A y = 16   k N

Fazendo agora o somatório das forças na horizontal, temos:

→ + ∑ F x = 0

A x = 0

Passo 3

Agora vamos traçar os diagramas de esforço cortante e de momento fletor.

Para traçar esses diagramas precisamos considerar intervalos, e esses intervalos são tomados de um ponto até outro onde o gráfico tende a mudar, seja por ação de uma força ou de uma reação.

Para A , temos:

↑ + ∑ F y = 0

V A - 16 = 0

V A = 16   k N

Sabemos que, entre A e C a área sob a curva da carga é zero, portanto:

V C - V A = 0

V C = 16   k N

Passo 4

Sabemos que:

d V d x = - w

Logo:

V D - V C = - 40

V D = - 24   k N

Agora vamos determinar o ponto, no qual o esforço cortante é zero. Temos:

V E - V C = w ⋅ u

0 - 16 = - 20 u

u = 0,8   m

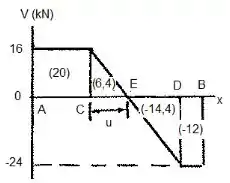
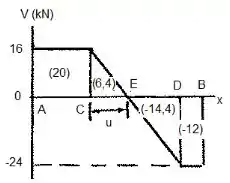
De posse destes valores, podemos construir o diagrama de esforço cortante, como no ponto no qual existem cargas localizadas e reações, a inclinação do diagrama de força cortante é nula.

Passo 5

A área sobre a curva do diagrama de força cortante, entre dois pontos, é igual à variação do momento fletor entre aqueles dois pontos. Para facilidade, calcula-se a área em cada trecho do diagrama de esforço cortante e anota-se o valor obtido no próprio diagrama.

Para A , temos:

M A = 0   k N ⋅ m

Assim, podemos escrever para o trecho A C :

M C - M A = 20

M C = 20   k N ⋅ m

Para o trecho C E :

M E - M C = 6,4 ⋅ m

M E = 26,4   k N ⋅ m

Para o trecho E D :

M E - M D = - 14,4   k N ⋅ m

M D = 12   k N ⋅ m

Para o trecho D B :

M B - M D = - 12

M B = 0   k N ⋅ m

De posse destes valores, podemos desenhar o diagrama de momento fletor:

Passo 6

Dos valores obtidos do gráfico de momento fletor e do esforço cortante, podemos obter:

Momento fletor absoluto máximo:

M m á x = 26,4   k N ⋅ m

Esforço cortante absoluto máximo:

V m á x = 24   k N

Resposta

a )   E s f o r ç o   C o r t a n t e :

M o m e n t o   f l e t o r :

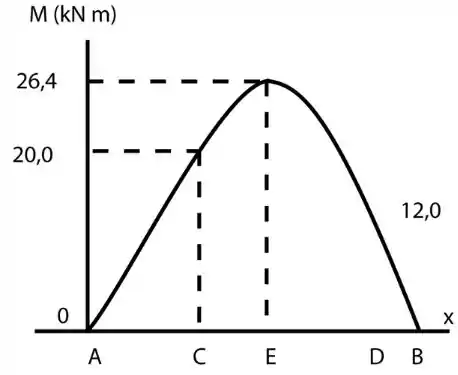
b ) Momento fletor absoluto máximo:

M m á x = 26,4   k N ⋅ m

Esforço cortante absoluto máximo:

V m á x = 24   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo A B C sustenta duas cargas tal como mostra a figura. Determine as distâncias a e b quando a força horizontal P de intensidade 270N é aplicada em A.
Sabendo que m B = 70k g e m C = 25k g , determine a intensidade da força P necessária para se manter o equilíbrio.
Se d C = 4,5m , determine a as distâncias d B e d D , b a máxima tensão no cabo.
Para a viga mostrada, determine (a) a intensidade P das duas forças concentradas para que o máximo valor absoluto do momento fletor seja o menor possivel, (b) o valor correspondente de M m á x á .
Para a viga e o carregamento mostrados na figura, (a) escreva as equações das curvas do esfroço cortante e do momento fletor, (b) determine o máximo momento fletor.