Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 83
Para a viga e carregamento mostrados na figura, trace os diagramas de esforço cortante e de momento fletor, determine a intensidade e localização do máximo valor absoluto do momento fletor.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiramente, vamos desenhar o diagrama de corpo livre considerando a carga distribuída:
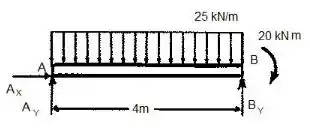
A carga concentrada devido a carga distribuída é igual a:
Portanto, temos o seguinte diagrama de corpo livre:
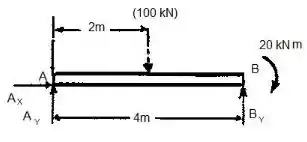
Passo 2
Vamos fazer o somatório dos momentos no ponto :
Fazendo agora o somatório das forças na horizontal, temos:
Passo 3
A força cortante, em qualquer ponto, é calculada a partir da divisão da viga em duas partes e da consideração de qualquer das partes como corpo livre.
Para :
Para que o diagrama esteja em equilíbrio, temos que:
O ponto , no qual o momento fletor é zero:
Passo 4
De posse destes valores, podemos construir o diagrama de esforço cortante, como no ponto no qual existem cargas localizadas e reações, a inclinação do diagrama de força cortante é nula.
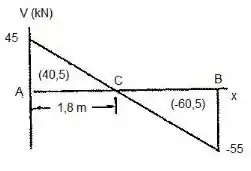
Passo 5
Para encontrar a equação do momento fletor, é necessário fazer o balanço do momento em cada seção.
Para traçar o diagrama do momento fletor, temos:
E como a variação do momento de até é igual a área do diagrama da cortante. Temos:
Para o trecho , teremos:
De posse destes valores, podemos desenhar o diagrama de momento fletor:
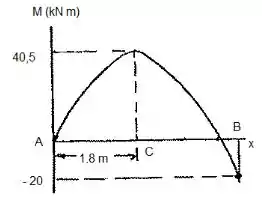
Passo 6
O momento máximo é localizado onde a cortante é igual a zero, e conforme o gráfico, ocorre a do ponto e tem valor igual a:
Resposta
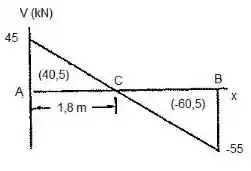
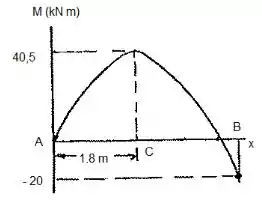
Momento fletor absoluto máximo:
Se localizando na distância de de .